建造一个容积为8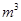
，深为2
的无盖水池，如果池底与池壁的造价每平方米分别是120元和80元，则水池的最低造价为 元.
科目：高中数学 来源： 题型：填空题
在平面直角坐标系xOy中，设定点A(a，a)，P是函数y＝
(x>0)图象上一动点．若点P，A之间的最短距离为2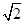
，则满足条件的实数a的所有值为________．
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
[2014·亳州模拟]若函数f(x)＝ax(a＞0，a≠1)在[－1,2]上的最大值为4，最小值为m，且函数g(x)＝(1－4m)
在[0，＋∞)上是增函数，则a＝________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，设池底宽为
，则长为
，则水池的造价为
。
,那么f(1)+f(2)+
=________.
的解集是 ．
的最小值为_________.
，
，
，
的图象如图
，则满足
的
取值范围是 .
)的定义域是(1，＋∞)，则实数a的值为________．