
已知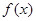 为
为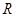 上的可导函数,且
上的可导函数,且 ,均有
,均有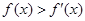 ,则有( )
,则有( )
A. ,
,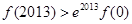
B. ,
,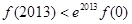
C. ,
,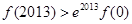
D. ,
,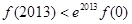
D
【解析】
试题分析:根据题目给出的条件:“f(x)为R上的可导函数,且对?x∈R,均有f(x)>f'(x)”,结合给出的四个选项,设想寻找一个辅助函数g(x)=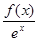 ,这样有以e为底数的幂出现,求出函数g(x)的导函数,由已知得该导函数大于0,得出函数g(x)为减函数,利用函数的单调性即可得到结论.解:令g(x)=
,这样有以e为底数的幂出现,求出函数g(x)的导函数,由已知得该导函数大于0,得出函数g(x)为减函数,利用函数的单调性即可得到结论.解:令g(x)=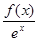 ,故
,故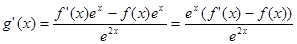 ,因为f(x)>f'(x),所以g′(x)<0,所以函数g(x)为R上的减函数,所以g(-2013)>g(0),所以e2013f(-2013)>f(0),f(2013)<e2013f(0).故选D.
,因为f(x)>f'(x),所以g′(x)<0,所以函数g(x)为R上的减函数,所以g(-2013)>g(0),所以e2013f(-2013)>f(0),f(2013)<e2013f(0).故选D.
考点:导数的运算
点评:本题考查了导数的运算,由题目给出的条件结合选项去分析函数解析式,属逆向思维,属中档题


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:2014届江西师大附中高三年级10月月考文科数学试卷(解析版) 题型:选择题
已知 为
为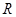 上的可导函数,当
上的可导函数,当 时,
时, ,则关于
,则关于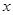 的函数
的函数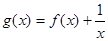 的零点个数为( )
的零点个数为( )
A.1 B.2 C.0 D.0或2
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省南阳市高三9月月考理科数学试卷(解析版) 题型:选择题
已知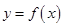 为
为 上的可导函数,当
上的可导函数,当 时,
时, ,则关于x的函数
,则关于x的函数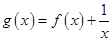 的零点个数为( )
的零点个数为( )
A.1 B.2 C.0 D.0或 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com