练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设f(x)=sin(w x＋j )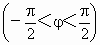给出以下四个论断：

    ①它的图象关于直线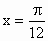对称；

    ②它的图象关于点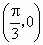对称；

    ③它的周期是π；

    ④它在区间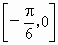上是增函数．

    以其中的两个论断作为条件，余下的两个论断作为结论，写出你认为正确的两个命题，并对其中一个命题加以证明．

    答案：略
    解析：

    解：两个正确命题如下：

    (1)；(2)．

    证明如下：

    (1)由③函数f(x)的周期为n得w =2．

    ∴f(x)=sin(2x＋j )．

    由①函数f(x)图象关于直线对称，则．又，即k=0，且，∴．∴．当时．∴f(x)的图象过点，即关于点对称，②成立．

    下面证明在上是增函数．

    由时f(x)为增函数．

    解得(kÎ Z)，即f(x)的增区间为

    (kÎ Z)．取k=0，得．又∴f(x)在内是增函数．∴④成立．由的证明略．

    综合运用y=Asin(w x＋j )的性质作出判断，然后运用讨论y=Asin(w x＋j )的性质的一般方法进一步讨论．


    提示：

    本题属于开放性命题，给定命题的条件，自己探索得出结论，需要有一定的结合分析推理能力，是近几年高考命题的新题型．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设f(x)=sin(2x+
    π
    6
    )+2msinxcosx，x∈R    ．
    （1）当m=0时，求f（x）在[0，
    π
    3
    ]    内的最小值及相应的x的值；
    （2）若f（x）的最大值为
    1
    2
    ，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f(x)=
    sin(
    π
    2
    x+
    π
    4
    )    		(x≤2008)
    f(x-5)(x＞2008)
    ，则f（2007）+f（2008）+f（2009）+f（2010）=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f(x)=
    sinπx(x＜0)
    f(x-1)+1(x≥0)
    ，g(x)=
    cosπx(x＜
    1
    2
    )
    g(x-1)+1(x≥
    1
    2
    )
    ，则g(
    1
    4
    )+f(
    1
    3
    )+g(
    5
    6
    )+f(
    3
    4
    )    的值为
    3
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f(x)=
    sinπx，(x＜0)
    f(x-1)+1(x≥0)
    ，g(x)=
    cosπx，(x＜
    1
    2
    )
    g(x-1)+1(x≥
    1
    2
    )
    ，则f(
    1
    3
    )+g(
    5
    6
    )    =
    2
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题中正确的是（　　）

    查看答案和解析>>

    同步练习册答案