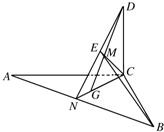
解:(1)在△ABC中,AC=BC,∠ACB=90
o故△ABC为等腰直角三角形
∵G为△ABC的重心,∴AB⊥GC①
又∵DC⊥平面ABC,AB平面ABC∴AB⊥DC②
由①②及DC∩GC=C知AB⊥面DGC,
∵DG?面DGC,∴AB⊥DG(6分)
(2)延长CG交AB于点N∵G为△ABC的重心∴N是AB的中点
∵∠ACB=90
o∴
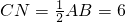
连接DN延长CM交DN于点C,由CN=DC=6,∠MCG=45
o知CE⊥DN,则E是DN的中点,连接BE,由AB⊥面DGC,知BE⊥CE
故∠BEN为二面角G-MC-B的平面角(9分)
在Rt△BEN中,BN=6,EN=

,∴
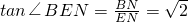
∴二面角G-MC-B的大小是
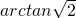
(12分)
分析:(1)欲证AB⊥DG,而DG?面DGC,故先证AB⊥面DGC,而AB⊥GC,AB⊥DC,DC∩GC=C,满足线面垂直的判定定理,从而问题得证;
(2)延长CG交AB于点N,G为△ABC的重心则N是AB的中点,连接DN延长CM交DN于点C,连接BE,根据二面角平面角的定义可知∠BEN为二面角G-MC-B的平面角,在Rt△BEN中,求出此角即可.
点评:本题主要考查了直线与平面垂直的性质,以及与二面角有关的立体几何综合题,同时考查了空间想象能力、运算求解能力、推理论证能力,考查数形结合思想、化归与转化思想,属于基础题.

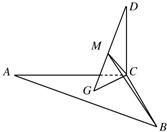 如图,△ABC中,∠C=90o,∠A=45o,DC⊥平面ABC,DC=6,G为△ABC的重心M为GD上的一点,∠MCG=45o.
如图,△ABC中,∠C=90o,∠A=45o,DC⊥平面ABC,DC=6,G为△ABC的重心M为GD上的一点,∠MCG=45o. 解:(1)在△ABC中,AC=BC,∠ACB=90o故△ABC为等腰直角三角形
解:(1)在△ABC中,AC=BC,∠ACB=90o故△ABC为等腰直角三角形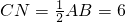
 ,∴
,∴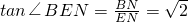
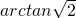 (12分)
(12分)

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案 如图,△ABC中,BC=2
如图,△ABC中,BC=2