
如图,在正方体
 中,设线段
中,设线段 与平面
与平面 交于Q,求证:
交于Q,求证: 三点共线.
三点共线.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014届浙江省高二10月月考文科数学试卷(解析版) 题型:解答题
如图,在正方体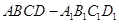 中,
中, 为底面
为底面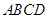 的中心,
的中心, 是
是 的中点,设
的中点,设 是
是 上的中点,求证:(1)
上的中点,求证:(1) ;
;
(2)平面 ∥平面
∥平面 .
.

查看答案和解析>>
科目:高中数学 来源:2013届江苏省高二4月月考理科数学试卷(解析版) 题型:解答题
如图,在正方体 中,
中,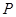 是棱
是棱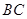 的中点,
的中点,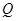 在棱
在棱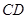 上.
上.
且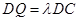 ,若二面角
,若二面角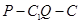 的余弦值为
的余弦值为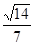 ,求实数
,求实数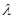 的值.
的值.
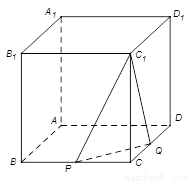
【解析】以A点为坐标原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,设正方体的棱长为4,分别求出平面C1PQ法向量和面C1PQ的一个法向量,然后求出两法向量的夹角,建立等量关系,即可求出参数λ的值.
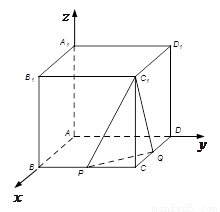
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com