
定义:已知函数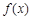 在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数
在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数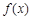 在[m,n]
(m<n)上具有“DK”性质.
在[m,n]
(m<n)上具有“DK”性质.
(1)判断函数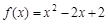 在[1,2]上是否具有“DK”性质,说明理由;
在[1,2]上是否具有“DK”性质,说明理由;
(2)若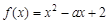 在[a,a+1]上具有“DK”性质,求a的取值范围.
在[a,a+1]上具有“DK”性质,求a的取值范围.
解:(1)∵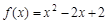 ,x∈[1,2],
,x∈[1,2],
∴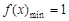 ≤1,
≤1,
∴函数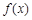 在[1,2]上具有“DK”性质……………………………………6分
在[1,2]上具有“DK”性质……………………………………6分
(2)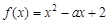 ,x∈[a,a+1],其对称轴为
,x∈[a,a+1],其对称轴为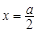 .
.
①当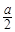 ≤a时,即a≥0时,函数
≤a时,即a≥0时,函数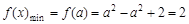 .
.
若函数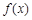 具有“DK”性质,则有2≤a总成立,即a≥2.…………8分
具有“DK”性质,则有2≤a总成立,即a≥2.…………8分
②当a<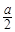 <a+1,即-2<a<0时,
<a+1,即-2<a<0时,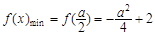 .
.
若函数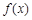 具有“DK”性质,则有
具有“DK”性质,则有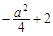 ≤a总成立,
≤a总成立,
解得a∈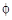 .…………………………………………………………………10分
.…………………………………………………………………10分
③当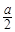 ≥a+1,即a≤-2时,函数
≥a+1,即a≤-2时,函数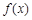 的最小值为
的最小值为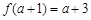 .
.
若函数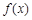 具有“DK”性质,则有a+3≤a,解得a∈
具有“DK”性质,则有a+3≤a,解得a∈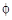 .………… 12分
.………… 12分
综上所述,若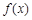 在[a,a+1]上具有“DK”性质,则a≥2.………… 14分
在[a,a+1]上具有“DK”性质,则a≥2.………… 14分
【解析】略


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省成都市高三第二次诊断性检测理科数学试卷(解析版) 题型:选择题
已知函数. (m为常数),对任意
(m为常数),对任意 ,均有
,均有 恒成立.下列说法:
恒成立.下列说法:
①若 为常数)的图象关于直线x=1对称,则b=1;
为常数)的图象关于直线x=1对称,则b=1;
②若 ,则必有
,则必有 ;
;
③已知定义在R上的函数 对任意X均有
对任意X均有 成立,且当
成立,且当 时,
时, ;又函数
;又函数 (c为常数),若存在
(c为常数),若存在 使得
使得 成立,则c的取值范围是(-1,13).其中说法正确的个数是
成立,则c的取值范围是(-1,13).其中说法正确的个数是
(A)3 个 (B)2 个 (C)1 个 (D)O 个
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省成都市高三第二次诊断性检测文科数学试卷(解析版) 题型:选择题
已知函数 (m为常数),对任意的
(m为常数),对任意的  恒成立.有下列说法:
恒成立.有下列说法:
①m=3;
②若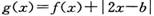 (b为常数)的图象关于直线x=1对称,则b=1;
(b为常数)的图象关于直线x=1对称,则b=1;
③已知定义在R上的函数F(x)对任意x均有 成立,且当
成立,且当 时,
时, ;又函数
;又函数 (c为常数),若存在
(c为常数),若存在 使得
使得 成立,则c的取值范围是(一1,13).
成立,则c的取值范围是(一1,13).
其中说法正确的个数是
(A)3 个 (B)2 个 (C)1 个 (D)O 个
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
定义:已知函数![]() 在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数
在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数![]() 在[m,n] (m<n)上具有“DK”性质.
在[m,n] (m<n)上具有“DK”性质.
(1)判断函数![]() 在[1,2]上是否具有“DK”性质,说明理由;
在[1,2]上是否具有“DK”性质,说明理由;
(2)若![]() 在[a,a+1]上具有“DK”性质,求a的取值范围.
在[a,a+1]上具有“DK”性质,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com