
分析 由已知X的可能取值为0,1,2,3,分别示求出相应的概率,由此能求出X的分布列.
解答 解:∵盒甲有16个白球和4个黑球,从中任意取出3个,X表示其中黑球的个数,
∴X的可能取值为0,1,2,3,
P(X=0)=$\frac{{C}_{16}^{3}}{{C}_{20}^{3}}$=$\frac{560}{1140}$=$\frac{28}{57}$,
P(X=1)=$\frac{{C}_{4}^{1}{C}_{16}^{2}}{{C}_{20}^{3}}$=$\frac{480}{1140}$=$\frac{24}{57}$,
P(X=2)=$\frac{{C}_{4}^{2}{C}_{16}^{1}}{{C}_{20}^{3}}$=$\frac{96}{1140}$=$\frac{8}{95}$,
P(X=3)=$\frac{{C}_{4}^{3}}{{C}_{20}^{3}}$=$\frac{4}{1140}$=$\frac{1}{285}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{28}{57}$ | $\frac{24}{57}$ | $\frac{8}{95}$ | $\frac{1}{285}$ |
点评 本题考查离散型随机变量的分布列的求法,是基础题,解题时要认真审题,注意排列组合知识的合理运用.


科目:高中数学 来源: 题型:填空题
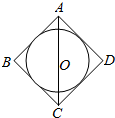 如图,圆O内切于正方形ABCD,将圆O、正方形ABCD绕直线AC旋转一周得到的两个旋转体的体积依次记为V1V2,则V1:V2=$\sqrt{2}:1$.
如图,圆O内切于正方形ABCD,将圆O、正方形ABCD绕直线AC旋转一周得到的两个旋转体的体积依次记为V1V2,则V1:V2=$\sqrt{2}:1$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
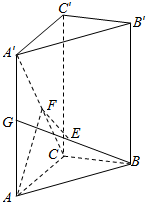 已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.
已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com