练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图,已知几何体的三视图,用斜二测画法画出它的直观图.


    解析:

    由几何体的三视图知道,这个几何体是一个简单组合体,它的下部是一个圆台,上部是一个圆锥,并且圆锥的底面与圆台的上底面重合,我们可以先画出下部的圆台,再画出上部的圆锥.

    画法:(1)画轴.如图(1),画x轴、y轴、z轴，使∠xOy=45°，∠xOz=90°.

    (2)画圆台的两底面.利用斜二测画法，画出底面⊙O，在z轴上截取OO′，使OO′等于三视图中相应高度，过O′作Ox的平行线O′x′，Oy的平行线O′y′，利用O′x与O′y′画出上底面⊙O′(与画⊙O一样).

    (3)画圆锥的顶点.在Oz上截取点P，使PO′等于三视图中相应的高度.

    (4)成图.连结PA′、PB′、A′A、B′B，整理得到三视图表示的几何体的直观图，如图(2).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

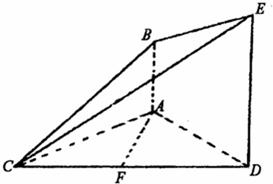    精英家教网如图，已知AB⊥平面ACD，DE∥AB，△ACD是正三角形，AD=DE=2AB=2，且F是CD的中点．
    （ I ）求证：AF∥平面BCE；
    （Ⅱ）求证：平面BCE⊥平面CDE．
    （Ⅲ）如果一只苍蝇在该几何体内部任意飞，求它在三棱锥B-ACF内部飞的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知图中的三个直角三角形是一个几何体的三视图，那么这个几何体的体积等于
    10
    10
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形，∠BAD=60°，AA1=6，P是棱AA1的中点．求：
    （1）截面PBD分这个棱柱所得的两个几何体的体积；
    （2）三棱锥A-PBD的高．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知三棱锥P-ABC的侧面PAC是底角为45°的等腰三角形，PA=PC，且该侧面垂直于底面，∠ACB=90°，AB=10，BC=6，B1C1=3．
    （1）求证：二面角A-PB-C是直二面角；
    （2）求二面角P-AB-C的正切值；
    （3）若该三棱锥被平行于底面的平面所截，得到一个几何体ABC-A1B1C1，求几何体ABC-A1B1C1的侧面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

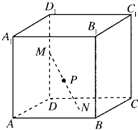    精英家教网如图，已知正方体ABCD-A1B1C1D1的棱长为a（a＞2），长度为2的线段MN的一个端点M在DD1上运动，另一端点N在底面ABCD上运动，则MN的中点P的轨迹（曲面）与共一顶点D的三个面所围成的几何体的体积为
     
    ．

    查看答案和解析>>

    同步练习册答案