
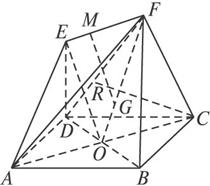
(1)求证:EO⊥平面AFC;
(2)在线段EF上找一点M,使三棱锥M—ACF为正三棱锥;
(3)试问在线段DF(不含端点)上是否存在一点R,使得CR∥平面ABF,若存在,请指出点R的位置;若不存在,请说明理由.
(1)证明:连结FO.设AB=BF=2DE=2a,则DO=OB=![]() a,所以EO=
a,所以EO=![]() a,FO=
a,FO=![]() a,EF=3a.
a,EF=3a.
在△EOF中,由EO2+FO2=EF2,知EO⊥FO.
又DE⊥平面ABCD,所以DE⊥AC,而BD⊥AC,所以AC⊥平面DOE,故AC⊥EO.
由AC![]() 面AFC,FO
面AFC,FO![]() 面AFC,AC∩FO=O,所以EO⊥平面AFC.
面AFC,AC∩FO=O,所以EO⊥平面AFC.
(2)解:在线段EF上取点M,使得EM∶MF=1∶2,此时三棱锥M—ACF为正三棱锥.
因为AF=FC=AC=2![]() a,
a,

所以△AFC是正三角形.
在线段OF上取点G,使得OG∶GF=1∶2,则点G是△AFC的重心,也就是△AFC的中心.
连结MG,则MG∥EO,由(1)得MG⊥平面AFC.
故此时三棱锥M—ACF为正三棱锥.
(3)解:找不到这样的点R,使得CR∥平面ABF.
假设存在这样的点R,使得CR∥平面ABF.
因为点R与点D不重合,所以CD与CR相交.
又CD∥平面ABF,CR∥平面ABF,且CR![]() 平面CDF,CD
平面CDF,CD![]() 平面CDF,所以平面CDF∥平面ABF.
平面CDF,所以平面CDF∥平面ABF.
而平面CDF与平面ABF有公共点F,所以平面CDF与平面ABF必定相交,矛盾.
所以找不到这样的点R,使得CR∥平面ABF.


科目:高中数学 来源: 题型:
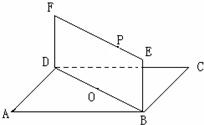 如图,已知正方形ABCD与矩形BEFD所在的平面互相垂直,AB=
如图,已知正方形ABCD与矩形BEFD所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
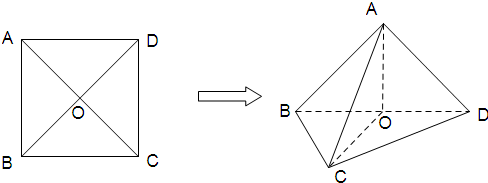
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证:EO⊥平面AFC.

(2)在线段EF上找一点M,使三棱锥M—ACF为正三棱锥.
(3)试问在线段DF(不含端点)上是否存在一点R,使得CR∥平面ABF?若存在,请指出点R的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011年湖南省长沙市长望浏宁四县市高三3月调研数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com