Question

(08年重庆卷文)（本小题满分12分，（Ⅰ）小问5分，（Ⅱ）小问7分.）

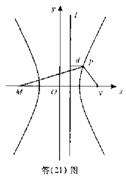
      如题（21）图，M（-2，0）和N（2，0）是平面上的两点，动点P满足：

                             

（Ⅰ）求点P的轨迹方程;

（Ⅱ）设d为点P到直线l： 的距离，若,求的值.

Answer 1

解：（I）由双曲线的定义，点P的轨迹是以M、N为焦点，实轴长2a=2的双曲线.

因此半焦距c=2，实半轴a=1，从而虚半轴b=,

所以双曲线的方程为x^2-=1.

(II)解法一：

由（I）由双曲线的定义，点P的轨迹是以M、N为焦点，实轴长2a=2的双曲线.

因此半焦距e=2，实半轴a=1，从而虚半轴b=.

R所以双曲线的方程为x²-=1.

(II)解法一：

由（I）及答（21）图，易知|PN|1,因|PM|=2|PN|²,       ①

知|PM|>|PN|,故P为双曲线右支上的点，所以|PM|=|PN|+2.     ②

将②代入①，得2||PN|²-|PN|-2=0，解得|PN|=,所以

|PN|=.

因为双曲线的离心率e==2,直线l:x=是双曲线的右准线，故=e=2,

所以d=|PN|,因此

解法：

 

设P（x,y），因|PN|1知

|PM|=2|PN|²2|PN|>|PN|,

故P在双曲线右支上，所以x1.

由双曲线方程有y²=3x²-3.

因此

从而由|PM|=2|PN|²得

2x+1=2(4x²-4x+1)，即8x²-10x+1=0.

所以x=(舍去x=).

有|PM|=2x+1=

d=x-=.

故