练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知α－β＝且α≠kπ(k∈Z).求的最大值及取最大值时的条件.

    令t＝－4sin2(－)

    ＝－4×

    ＝－4×(－sin)

    ＝2(sin＋sin)－2＝4sincos－2，

    ∵α－β＝π，∴＝＝－.

    ∴t＝4sin(－π)×(－)－2

    ＝－2sin(－)－2，

    ∵α≠kπ(k∈Z)，∴－π≠－(k∈Z)，

    当－＝2kπ－，即α＝4kπ＋(k∈Z)时，

    tmax＝－2×(－1)－2＝0.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：新课标教材全解高中数学人教A版必修1 人教A版 题型：044

    已知：集合M＝{x|k＋1≤x≤2k}，N＝{x|1≤x≤3}，且MN．求k取值范围．

    查看答案和解析>>

    科目：高中数学 来源：河南省镇平一高2012届高三下学期第三次周考数学文科试题 题型：013

    已知函数f(x)＝＋k定义域为D，且方程f(x)＝x在D上有两个不等实根，则k的取值范围是

    [　　]

    A．k＜1

    B．≤k＜1

    C．k＞－1

    D．

    －1＜k≤－

    查看答案和解析>>

    科目：高中数学 来源：江苏省栟茶高级中学2012届高三第一次学情调研测试数学试题 题型：044

    已知函数f(x)＝lg(k∈R且k＞0)．

    (1)求函数f(x)的定义域；

    (2)若函数f(x)在[10，＋∞)上是单调增函数，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)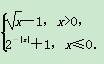＝若关于x的方程f(x)＋2x－k＝0有且只有两个不同的实根，则实数k的取值范围为                                        (　　)

    A．(－1,2]                         B．(－∞，1]∪(2，＋∞)

    C．(0,1]                           D．[1，＋∞)

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江西赣州四所重点中学高三上学期期末联考理数学试卷（解析版） 题型：解答题

    已知函数f(x)＝在x＝0，x＝处存在极值。

    （Ⅰ）求实数a,b的值；

    （Ⅱ）函数y＝f(x)的图象上存在两点A,B使得△AOB是以坐标原点O为直角顶点的直角三角形，且斜边AB的中点在y轴上，求实数c的取值范围；

    (Ⅲ）当c＝e时，讨论关于x的方程f(x)＝kx(k∈R)的实根个数。

     

    查看答案和解析>>

    同步练习册答案