
 +2-2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.
+2-2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.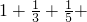 …+
…+ >
>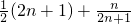 (n∈N+)
(n∈N+)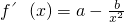 ,根据题意f′(1)=a-b=2,即b=a-2 …3分
,根据题意f′(1)=a-b=2,即b=a-2 …3分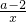 +2-2a,
+2-2a,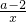 +2-2a-2lnx,x∈[1,+∞)
+2-2a-2lnx,x∈[1,+∞)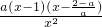
 ,
,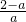 ,则g′(x)<0,g(x)在[1,+∞)减函数,所以g(x)<g(1)=0,即f(x)≥2lnx在[1,+∞)上恒不成立.
,则g′(x)<0,g(x)在[1,+∞)减函数,所以g(x)<g(1)=0,即f(x)≥2lnx在[1,+∞)上恒不成立.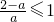 ,当x>1时,g′(x)>0,g(x)在[1,+∞)增函数,又g(1)=0,所以f(x)≥2lnx.
,当x>1时,g′(x)>0,g(x)在[1,+∞)增函数,又g(1)=0,所以f(x)≥2lnx.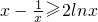 ,令
,令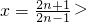 1得
1得 ,
,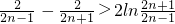

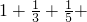 …+
…+ >
>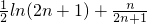 (n∈N+)…13分.
(n∈N+)…13分.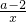 +2-2a,构造新函数g(x)=f(x)-2lnx=ax+
+2-2a,构造新函数g(x)=f(x)-2lnx=ax+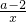 +2-2a-2lnx,x∈[1,+∞)则g(1)=0,g′(x)=
+2-2a-2lnx,x∈[1,+∞)则g(1)=0,g′(x)=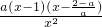 ,比较对应方程根的大小,进行分类讨论,即可求得a的取值范围;
,比较对应方程根的大小,进行分类讨论,即可求得a的取值范围;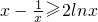 ,令
,令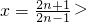 1,从而可得
1,从而可得 ,进而可得结论.
,进而可得结论.

科目:高中数学 来源: 题型:
| f(b) |
| a |
| f(a) |
| b |
| 1 |
| 2 |
| f(2n) |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| b |
| x |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2 |
| n |
| 2n+1 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省武汉中学高三(上)10月月考数学试卷(文科)(解析版) 题型:解答题
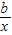 +2-2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.
+2-2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.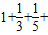 …+
…+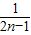 >
>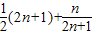 (n∈N+)
(n∈N+)查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省黄石市大冶市华中学校高三数学滚动训练(二)(解析版) 题型:解答题
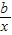 +2-2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.
+2-2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.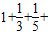 …+
…+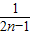 >
>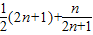 (n∈N+)
(n∈N+)查看答案和解析>>
科目:高中数学 来源:2009-2010学年上海市浦东新区建平中学高三(上)12月月考数学试卷(文理合卷)(解析版) 题型:填空题
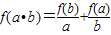 ,
,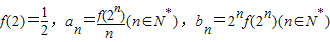 ,考查下列结论:
,考查下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com