
已知曲线![]() :
:![]() ,数列
,数列![]() 的首项
的首项![]() ,且当
,且当![]() 时,点
时,点![]() 恒在曲线
恒在曲线![]() 上,数列
上,数列![]() 满足
满足![]() .
.
(1)试判断数列![]() 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;
(2)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(3)设数列![]() 满足
满足![]() ,试比较数列
,试比较数列![]() 的前n项和
的前n项和![]() 与2的大小.
与2的大小.
(1)数列![]() 是公差为
是公差为![]() 的等差数列.
的等差数列.
(2)![]() ;
; ![]()
(3)![]()
![]()
(1)∵当![]() 时,点
时,点![]() 恒在曲线
恒在曲线![]() 上
上
∴![]() -----------------------------------------------1分
-----------------------------------------------1分
由![]() 得
得
当![]() 时,
时,![]()
![]()
![]()
![]() ----5分
----5分
∴数列![]() 是公差为
是公差为![]() 的等差数列.-------------------------------------------------------6分
的等差数列.-------------------------------------------------------6分
(2)∵![]() =4,∴
=4,∴![]()
∴![]() -----------------------------------8分
-----------------------------------8分
由![]() 得
得![]() -----------------------------------------------10分
-----------------------------------------------10分
(3)∵![]() ∴
∴![]() =
=![]() ----------------------12分
----------------------12分
∴![]()
![]()
![]() -----14分
-----14分


科目:高中数学 来源: 题型:
| 1 | an-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
已知曲线![]() :
:![]() ,数列
,数列![]() 的首项
的首项![]() ,且当
,且当![]() 时,点
时,点![]() 恒在曲线
恒在曲线![]() 上,数列
上,数列![]() 满足
满足![]() .
.
(1)试判断数列![]() 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;
(2)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(3)设数列![]() 满足
满足![]() ,试比较数列
,试比较数列![]() 的前n项和
的前n项和![]() 与2的大小.
与2的大小.
查看答案和解析>>
科目:高中数学 来源:广东省揭阳市2010年高考一模(文) 题型:解答题
(本题满分14分)
已知曲线 :
: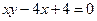 ,数列
,数列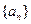 的首项
的首项 ,且当
,且当 时,点
时,点 恒在曲线
恒在曲线 上,数列
上,数列 满足
满足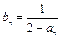 .
.
(1)试判断数列 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;
(2)求数列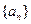 和
和 的通项公式;
的通项公式;
(3)设数列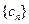 满足
满足 ,试比较数列
,试比较数列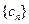 的前n项和
的前n项和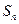 与2的大小.
与2的大小.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省高三第四次月考理科数学试题(解析版) 题型:解答题
(本小题满分14分)
已知曲线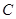 :
: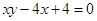 ,数列
,数列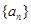 的首项
的首项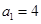 ,且当
,且当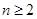 时,点
时,点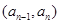 恒在曲线
恒在曲线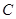 上,数列
上,数列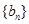 满足
满足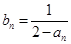 。
。
(1)试判断数列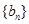 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;
(2)求数列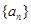 和
和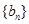 的通项公式;
的通项公式;
(3)设数列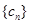 满足
满足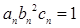 ,试比较数列
,试比较数列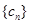 的前
的前 项和
项和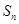 与2的大小。
与2的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com