Question

已知几何体A-BCDE的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．
（1）若几何体A-BCDE的体积为16，求实数a的值；
（2）若a=1，求异面直线DE与AB所成角的余弦值；
（3）是否存在实数a，使得二面角A-DE-B的平面角是45°，若存在，请求出a值；若不存在请说明理由．

Answer 1

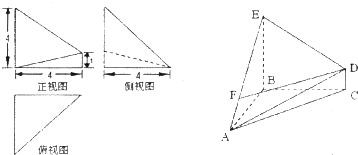
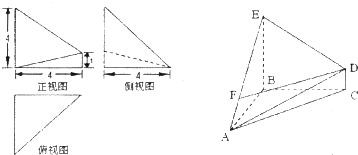
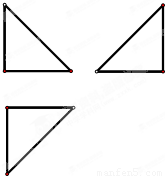
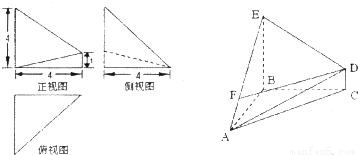
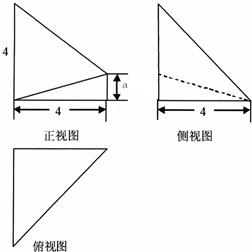
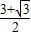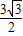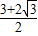解：（1）由该几何体的三视图知AC⊥面BCED，
且EC=BC=AC=4，BD=a，
∵几何体A-BCDE的体积为16，
∴，
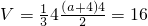
解得a=2；
（2）解一：过点B作BF∥ED交EC于F，连接AF，
则∠FBA或其补角即为异面直线DE与AB所成角，
在△BAF中，，，
∴；
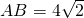
即异面直线DE与AB所成角的余弦值为．
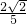
解二：以C为原点，以CA、CB、CE所在直线为x、y、z轴建立如图所示的空间直角坐标系，
则A（4，0，0），B（0，4，0），D（0，4，1），E（0，0，4），
得，，
，
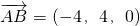
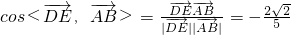
又异面直线DE与AB所成角为锐角，
可得异面直线DE与AB所成角的余弦值为．
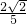
（3）以C为原点，以CA、CB、CE所在直线为x、y、z轴建立如图所示的空间直角坐标系，
则A（4，0，0），B（0，4，0），D（0，4，a），E（0，0，4），
平面BDE的法向量，
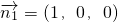
平面ADE的法向量，，，
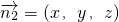
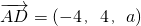
由，
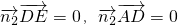
可得，
，
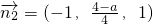
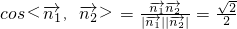
∵a=4．
此时，与正视图为直角梯形条件不符，所以舍去，
因此不存在实数a，使得二面角A-DE-B的平面角是45°．
分析：（1）由该几何体的三视图知AC⊥面BCED，且EC=BC=AC=4，BD=a，由几何体A-BCDE的体积为16，构造关于a的方程解方程可得答案．
（2）求异面直线所成的角，一般有两种方法，
解一是几何法，其基本解题思路是“异面化共面，认定再计算”，即利用平移法和补形法将两条异面直线转化到同一个三角形中，结合余弦定理来求．过点B作BF∥ED交EC于F，连接AF，则∠FBA或其补角即为异面直线DE与AB所成角；
解二是向量法，以C为原点，以CA、CB、CE所在直线为x、y、z轴建立如图所示的空间直角坐标系分别求出异面直线DE与AB的方向向量代入向量夹角公式，可得答案．
（3）以C为原点，以CA、CB、CE所在直线为x、y、z轴建立如图所示的空间直角坐标系，求出平面BDE的法向量和平面ADE的法向量根据二面角A-DE-B的平面角是45°，构造关于a的方程，判断方程是否有解可得答案．
点评：本题考查的知识点是与二面角有关的立体几何综合应用，由三视图求面积，异面直线及其所成的角，难度比较大，熟练掌握几何法及向量法求夹角的方法和步骤是解答本题的关键．
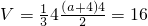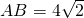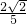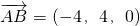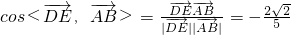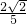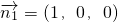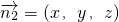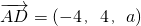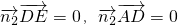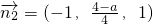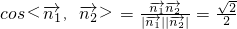