分析:(1)以D点为坐标原点,DA为x轴,DC为y轴,DD
1为z轴,建立空间直角坐标系D-xyz,先求出平面ABCD的一个法向量为
,设EF与
的夹角为θ,求出此角的余弦值,根据EF与平面ABCD所成的角与θ互补求出所求即可;
(2)先求出
与
的坐标,设平面DEF的一个法向量为m,则m•
=0,m•
=0,建立两个等式关系,求出m,利用两法向量的夹角公式求出cos<m,n>,即可得到二面角F-DE-C的余弦值.
解答: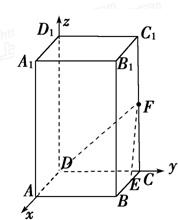
解:建立如图所示的空间直角坐标系D-xyz,则D(0,0,0),A(2,0,0),C(0,2,0),B(2,2,0),E(1,2,0),F(0,2,2).
(1)
=(-1,0,2).
易得平面ABCD的一个法向量为n=(0,0,1),
设EF与n的夹角为θ,
则cosθ═
,
∴EF与平面ABCD所成的角的余弦值为
.
(2)
=(-1,0,2),
=(0,2,2).
设平面DEF的一个法向量为m,则m•
=0,m•
=0,
可得m=(2,-1,1),∴cos<m,n>=
=
,
∴二面角F-DE-C的余弦值为
.
点评:本题主要考查了直线与平面所成的角,以及二面角等基础知识,考查空间想象能力,运算能力和推理论证能力,属于中档题.

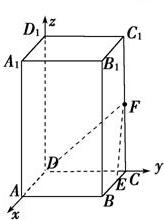 如图,在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4,E为BC的中点,F为CC1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4,E为BC的中点,F为CC1的中点. 解:建立如图所示的空间直角坐标系D-xyz,则D(0,0,0),A(2,0,0),C(0,2,0),B(2,2,0),E(1,2,0),F(0,2,2).
解:建立如图所示的空间直角坐标系D-xyz,则D(0,0,0),A(2,0,0),C(0,2,0),B(2,2,0),E(1,2,0),F(0,2,2).

 如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点.
如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点. 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′= (2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=
(2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1= 如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点. (2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )
(2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )