
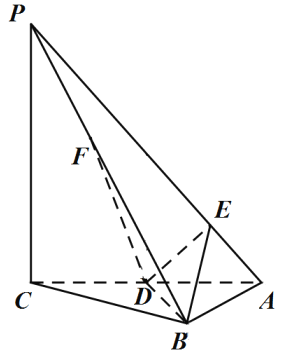
【题目】如图,在三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 是棱
是棱![]() 的中点,
的中点,![]() ,点
,点![]() 是棱
是棱![]() 上一点,且
上一点,且![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)证明![]() 平面
平面![]() ,可得出
,可得出![]() ,再证明
,再证明![]() 可得出
可得出![]() ,利用线面垂直的判定定理可得出结论;
,利用线面垂直的判定定理可得出结论;
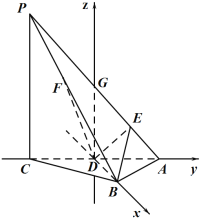
(2)过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,然后以点
,然后以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,计算出
,计算出![]() 的坐标,并计算出平面
的坐标,并计算出平面![]() 的法向量,利用空间向量法能计算出直线
的法向量,利用空间向量法能计算出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)因为![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,又
,又![]() ,
,![]() 平面
平面![]() ;
;
(2)因为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() ,故可以
,故可以![]() 、
、![]() 、
、![]() 分别作为
分别作为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则部分点坐标为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
因为点![]() 在棱
在棱![]() 上,且
上,且![]() ,则
,则![]() ,
,
则![]() ,即有
,即有![]() ,即
,即 ,
,
由(1)知![]() 平面
平面![]() ,则
,则![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则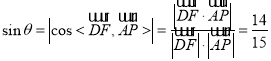 ,
,
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重![]() ,次品重
,次品重![]() ,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第
,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() ),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() _________
_________![]() ;若次品所在的袋子的编号是
;若次品所在的袋子的编号是![]() ,此时的重量
,此时的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质检部门为了解某企业生产的一-种圆柱形零件的质量情况,随机抽检了100个零件,得到这些零件的横截面直径d(单位:![]() )的频率分布表如下:
)的频率分布表如下:
d的分组 |
|
|
|
|
|
零件数 | 12 | 38 | 38 | 10 | 2 |
(1)试估计这个企业生产的这类零件的横截面直径不低于![]() 的概率;
的概率;
(2)求这个企业生产的这类零件的横截面直径的平均数与标准差的估计值(同一组中的数据用该区间的中点值为代表).(精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如:第三季度华为销量约占50%,苹果销量约占20%,三星销量约占30%).根据该图,以下结论中一定正确的是( )
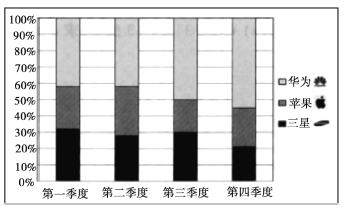
A.华为的全年销量最大B.苹果第二季度的销量大于第三季度的销量
C.华为销量最大的是第四季度D.三星销量最小的是第四季度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2acoskπlnx(k∈N*,a∈R且a>0).
(1)讨论函数f(x)的单调性;
(2)若k=2018,关于x的方程f(x)=2ax有唯一解,求a的值;
(3)当k=2019时,证明:对一切x∈(0,+∞),都有![]() 成立.
成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com