
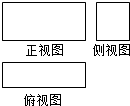
 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )| A. | 3$\sqrt{5}$+2 | B. | 6$\sqrt{5}$+4 | C. | 6 | D. | 10 |
分析 设长方体的长,宽,高分别为x,y,z,根据已知求出长宽高,代入长方体表面积公式,可得答案.
解答 解:设长方体的长,宽,高分别为x,y,z,
由题意得:$\left\{\begin{array}{l}\sqrt{{x}^{2}+{y}^{2}+{z}^{2}}=\sqrt{10}\\ \sqrt{{x}^{2}+{z}^{2}}=\sqrt{6}\\ \sqrt{{y}^{2}+{z}^{2}}=\sqrt{5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=\sqrt{5}\\ y=2\\ z=1\end{array}\right.$,
故该长方体的表面积S=2(xy+xz+yz)=6$\sqrt{5}$+4,
故选:B.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {$\frac{{e}^{2}}{3}$} | B. | (0,$\frac{{e}^{2}}{3}$) | C. | ($\frac{{e}^{2}}{3}$,e) | D. | ($\frac{1}{e}$,1)∪{$\frac{{e}^{2}}{3}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈R,2x>0”的否定是“?x0∈R,2${\;}^{{x}_{0}}$<0” | |
| B. | 命题“若sinx=siny,则x=y”的逆否命题为真命题 | |
| C. | 若命题p,¬q都是真命题,则命题“p∧q”为真命题 | |
| D. | 命题“若△ABC为锐角三角形,则有sinA>cosB”是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com