(13分)记
(1)计算f(1)、f(2)、f(3)、f(4)(2)猜想f(n)表达式，并用数字归纳法证明.
科目：高中数学 来源： 题型：
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
查看答案和解析>>
科目：高中数学 来源：2011-2012学年重庆市高三下学期第一次月考理科数学 题型：解答题
（本小题满分13分，（1）小问6分，（2）小分7分.）
进行一次掷骰子放球游戏，规定：若掷出1点，甲盒中放一球；若掷出2点或3点，乙
盒中放一球；若掷出4点或5点或6点，丙盒中放一球，共掷4次.
（1）求丙盒中至少放3个球的概率；
（2）记甲、乙两盒中所放球的总数为随机变量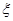
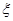，求的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源：2010-2011学年北京市海淀区高三下学期期中考试数学理卷 题型：解答题
（本小题共13分）
某厂生产的产品在出厂前都要做质量检测，每一件一等品都能通过检测，每一件二等品通过检测的概率为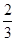
.现有10件产品，其中6件是一等品，4件是二等品.
(Ⅰ) 随机选取1件产品，求能够通过检测的概率；
(Ⅱ)随机选取3件产品，其中一等品的件数记为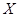
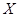，求的分布列；
(Ⅲ) 随机选取3件产品，求这三件产品都不能通过检测的概率.
查看答案和解析>>
科目：高中数学 来源：2010-2011学年北京市房山区高三统练数学理卷 题型：解答题
（本小题共13分）
某同学设计一个摸奖游戏：箱内有红球3个，白球4个，黑球5个．每次任取一个，有放回地抽取3次为一次摸奖．至少有两个红球为一等奖，记2分；红、白、黑球各一个为二等奖，记1分；否则没有奖，记0分．
（I）求一次摸奖中一等奖的概率；
（II）求一次摸奖得分的分布列和期望．
查看答案和解析>>
科目：高中数学 来源：2014届湖南省高一下学期期中联考数学试卷（解析版） 题型：解答题
箱子里有3双不同的手套，随机地拿出2只，记事件A={拿出的手套配不成对}；事件B={拿出的都是同一只手上的手套}；事件C={拿出的手套一只是左手的，一只是右手的，但配不成对}。（本小题满分13分）
（1）请罗列出所有的基本事件；
（2）分别求事件A、事件B、事件C的概率；
（3）说出事件A、事件B、事件C的关系。
【解析】第一问利用分别设3双手套为：
；
；
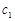
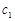。 、、分别代表左手手套，、、分别代表右手手套。
第二问①事件A包含12个基本事件，故P（A）=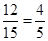 
，（或能配对的只有3个基本事件，
P（A）=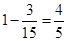 
）；
②事件B包含6个基本事件，故P(B)=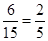 
；
事件C包含6个基本事件，故P(C)=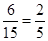
第三问
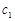
解：（1）分别设3双手套为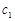：；；。 、、分别代表左手手套，、、分别代表右手手套。…………2分
箱子里 的3双不同的手套，随机地拿出2只，所有的基本事件是：
（，）、（，
）、（，）、（，）、（，）
（ ，）、（，）、（，
）、(，)；
（，）、（，）、（，）
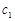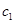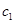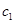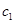（，）、（，）、（，） 共15个基本事件。 ……………5分
(2)①事件A包含12个基本事件，故P（A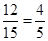）= ，（或能配对的只有3个基本事件，
P（A）= ）；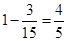
……………7分
②事件B包含6个基本事件，故P(B)= 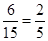；…………9分
③事件C包含6个基本事件，故P(C)= 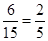。…………11分
⑶
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，f(2)=
，f(3)=
，f(4)=
(4分)
(6分)
)时，猜想成立
…＋
(8分)
(11分)
时一切正整数都成立. (13分)
