
【题目】有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次.根据年龄将大众评委分为五组,各组的人数如下:
组别 | A | B | C | D | E |
人数 | 50 | 100 | 150 | 150 | 50 |
(1)为了调查评委对7位歌手的支持情况,现用分层抽样方法从各组中抽取若干评委,其中从B组抽取了6人,请将其余各组抽取的人数填入下表.
组别 | A | B | C | D | E |
人数 | 50 | 100 | 150 | 150 | 50 |
抽取人数 | 6 |
(2)在(1)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.
【答案】(1) 如下表:
组别 | A | B | C | D | E |
人数 | 50 | 100 | 150 | 150 | 50 |
抽取人数 | 3 | 6 | 9 | 9 | 3 |
(2) ![]()
【解析】试题(1)分层抽样是按照每一层的个体数之比进行抽样,易得A、C、D、E四组抽取的人数;(2)由(1)知A组抽取3人其中有2人支持1号歌手,B组抽取6人其中2人支持1号歌手.运用列举法知,从这两组被抽到的评委中分别任选1人共有18种不同的结果,其中这两人都支持1号歌手的共有4种不同的结果,然后由古典概型的概率计算即可求解.
试题解析:(1)由题设知,分层抽样的抽取比例为6%,所以各组抽取的人数如下表:
组别 | A | B | C | D | E |
人数 | 50 | 100 | 150 | 150 | 50 |
抽取人数 | span>3 | 6 | 9 | 9 | 3 |
(2)记从A组抽到的3个评委为a1,a2,a3,其中a1,a2支持1号歌手;从B组抽到的6个评委为b1,b2,b3,b4,b5,b6,其中b1,b2支持1号歌手.从{a1,a2,a3}和{b1,b2,b3,b4,b5,b6}中各抽取1人的所有结果为:

由以上树状图知所有结果共18种,其中2人都支持1号歌手的有a1b1,a1b2,a2b1,a2b2共4种,故所求概率p=![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求证:函数f(x)-g(x)必有零点;
(2)设函数G(x)=f(x)-g(x)-1
①若函数G(x)有两相异零点且![]() 在
在![]() 上是减函数,求实数m的取值范围。
上是减函数,求实数m的取值范围。
②是否存在整数a,b使得![]() 的解集恰好为
的解集恰好为![]() 若存在,求出a,b的值,若不存在,请说明理由。
若存在,求出a,b的值,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但蔬菜上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水![]() (单位:千克)清洗蔬菜
(单位:千克)清洗蔬菜![]() 千克后,蔬菜上残留的农药
千克后,蔬菜上残留的农药![]() (单位:微克)的统计表:
(单位:微克)的统计表:
|
|
|
|
|
|
|
|
|
|
|
|
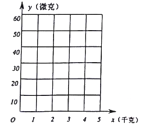
(1)在下面的坐标系中,描出散点图,并判断变量![]() 与
与![]() 是正相关还是负相关;
是正相关还是负相关;
(2)若用解析式![]() 作为蔬菜农药残量
作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程,令
的回归方程,令![]() ,计算平均值
,计算平均值![]() 与
与![]() ,完成以下表格(填在答题卡中),求出
,完成以下表格(填在答题卡中),求出![]() 与
与![]() 的回归方程.(
的回归方程.(![]() 保留两位有效数字);
保留两位有效数字);
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
(3)对于某种残留在蔬菜上的农药,当它的残留量低于![]() 微克时对人体无害,为了放心食用该蔬菜,请评估需要用多少千克的清水清洗一千克蔬菜?(精确到
微克时对人体无害,为了放心食用该蔬菜,请评估需要用多少千克的清水清洗一千克蔬菜?(精确到![]() ,参考数据
,参考数据![]() )(附:对于一组数据
)(附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: 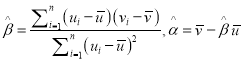 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人玩猜数字游戏,先由甲心中任想一个数字记为![]() ,再由乙猜甲刚才想的数字,把乙猜的数字记为
,再由乙猜甲刚才想的数字,把乙猜的数字记为![]() ,且
,且![]() 、
、![]() .若
.若![]() ,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用![]() ,
,![]() ,
,![]() 表示空间中三条不同的直线,
表示空间中三条不同的直线,![]() 表示平面, 给出下列命题:
表示平面, 给出下列命题:
① 若![]() ,
,![]() , 则
, 则![]() ∥
∥![]() ; ② 若
; ② 若![]() ∥
∥![]() ,
,![]() ∥
∥![]() , 则
, 则![]() ∥
∥![]() ;
;
③ 若![]() ∥
∥![]() ,
,![]() ∥
∥![]() , 则
, 则![]() ∥
∥![]() ; ④ 若
; ④ 若![]()
![]()
![]() ,
,![]()
![]()
![]() , 则
, 则![]() ∥
∥![]() .
.
其中真命题的序号是( )
A. ①② B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱载堉(1536—1611),明太祖九世孙,音乐家、数学家、天文历算家,在他多达百万字的著述中以《乐律全书》最为著名,在西方人眼中他是大百科全书式的学者王子。他对文艺的最大贡献是他创建了“十二平均律”,此理论被广泛应用在世界各国的键盘乐器上,包括钢琴,故朱载堉被誉为“钢琴理论的鼻祖”。“十二平均律”是指一个八度有13个音,相邻两个音之间的频率之比相等,且最后一个音频率是最初那个音频率的2倍,设第二个音的频率为![]() ,第八个音的频率为
,第八个音的频率为![]() ,则
,则![]() 等于
等于
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com