
 +
+ -
-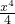 +…-
+…-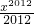 +
+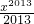 ) cos2x在区间[-3,3]上的零点的个数为
) cos2x在区间[-3,3]上的零点的个数为 +
+ -
-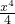 +…-
+…-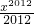 +
+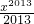 和y=cos2x的积,分别计算这两个函数的零点.前面的用导数证明是单调增,且f(-3)f(3)<0,所以必有一个零点;后面一个函数y=cos2x的零点是四个,从而得出答案.
和y=cos2x的积,分别计算这两个函数的零点.前面的用导数证明是单调增,且f(-3)f(3)<0,所以必有一个零点;后面一个函数y=cos2x的零点是四个,从而得出答案. +
+ -
-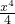 +…-
+…-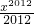 +
+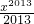 ,则g′(x)=1-x+x2-x3+…+x2012=
,则g′(x)=1-x+x2-x3+…+x2012=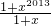 ,
,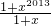 >0,故函数g(x)在[-3,3]上是增函数,
>0,故函数g(x)在[-3,3]上是增函数,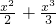 )+(-
)+(-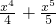 )+…+(-
)+…+(-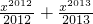 )>0,
)>0, +
+ -
-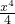 +…-
+…-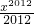 +
+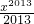 )cos2x在区间[-3,3]上的零点的个数为1+4=5.
)cos2x在区间[-3,3]上的零点的个数为1+4=5.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com