
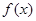 的图象在
的图象在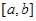 上连续,定义:
上连续,定义: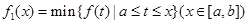 ,
,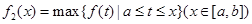 .其中,
.其中,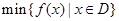 表示函数
表示函数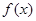 在
在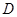 上的最小值,
上的最小值,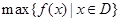 表示函数
表示函数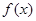 在
在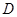 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数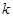 ,使得
,使得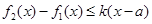 对任意的
对任意的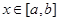 成立,则称函数
成立,则称函数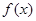 为
为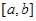 上的“
上的“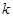 阶收缩函数”.
阶收缩函数”.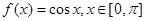 ,试写出
,试写出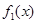 ,
,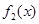 的表达式;
的表达式;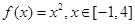 ,试判断
,试判断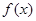 是否为
是否为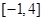 上的“
上的“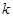 阶收缩函数”.如果是,求出对应的
阶收缩函数”.如果是,求出对应的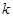 ;如果不是,请说明理由;
;如果不是,请说明理由;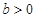 ,函数
,函数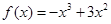 是
是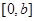 上的2阶收缩函数,求
上的2阶收缩函数,求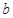 的取值范围.
的取值范围.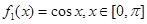 ,
,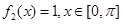 ;(Ⅱ)存在k=4,使得f(x)是[﹣1,4]上的4阶收缩函数.(Ⅲ)
;(Ⅱ)存在k=4,使得f(x)是[﹣1,4]上的4阶收缩函数.(Ⅲ)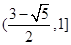
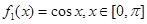 ,
,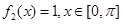 2分
2分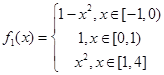 ,
,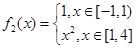 ,
,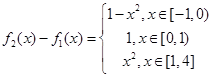 4分
4分 时,
时,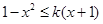 ,∴
,∴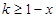 ,即
,即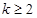 ;
;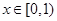 时,
时,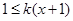 ,∴
,∴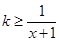 ,即
,即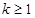 ;
;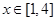 时,
时,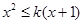 ,∴
,∴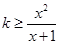 ,即
,即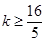 .
.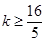
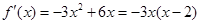 令
令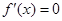 得
得 或
或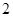 .函数f(x)的变化情况如下:
.函数f(x)的变化情况如下:| x | (-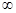 ,0) ,0) | 0 | (0,2) | 2 | (2,+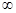 ) ) |
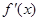 | - | 0 | + | 0 | - |
| f(x) |  | 0 |  | 4 |  |
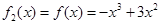 ,
,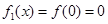 .
.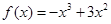 是[0,b]上的2阶收缩函数,所以,①
是[0,b]上的2阶收缩函数,所以,①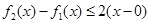 对x∈[0,b]恒成立;②存在x∈[0,b],使得
对x∈[0,b]恒成立;②存在x∈[0,b],使得 成立.
成立.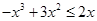 对x∈[0,b]恒成立,由
对x∈[0,b]恒成立,由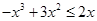 ,解得:0≤x≤1或x≥2,
,解得:0≤x≤1或x≥2,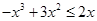 对x∈[0,b]恒成立,需且只需0<b≤1.
对x∈[0,b]恒成立,需且只需0<b≤1.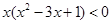 成立.由
成立.由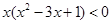 得:x<0或
得:x<0或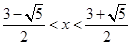 ,所以
,所以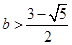 .
.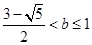 . 10分
. 10分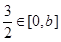 ,由于f(x)在[0,2]上单调递增,根据定义可得:
,由于f(x)在[0,2]上单调递增,根据定义可得: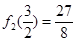 ,
,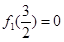 ,可得
,可得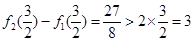 ,
,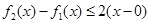 不成立. 12分
不成立. 12分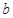 的取值范围为
的取值范围为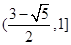 . 13分
. 13分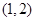 内的一个数来构造反例即可,这里用
内的一个数来构造反例即可,这里用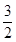 只是因为简单而已)
只是因为简单而已)

科目:高中数学 来源:不详 题型:解答题
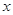 个月顾客对某种商品的需求总量
个月顾客对某种商品的需求总量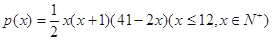 (单位:件)
(单位:件)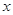 个月的需求量
个月的需求量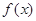 的表达式;
的表达式;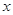 个月的销售量
个月的销售量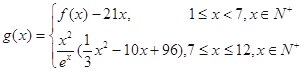 (单位:件),每件利润
(单位:件),每件利润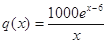 (单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据:
(单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据: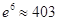 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,恒过定点
,恒过定点 .
. ;
; 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移 个单位后得到函数
个单位后得到函数 ,设函数
,设函数 的反函数为
的反函数为 ,直接写出
,直接写出 的解析式;
的解析式; 上的函数
上的函数 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
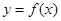 在区间
在区间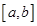 上存在
上存在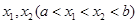 ,满足
,满足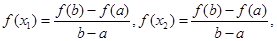 则称函数
则称函数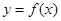 在区间
在区间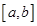 上的一个双中值函数,已知函数
上的一个双中值函数,已知函数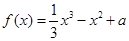 是区间
是区间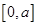 上的双中值函数,则实数
上的双中值函数,则实数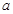 的取值范围是 ( )
的取值范围是 ( )A.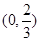 | B.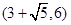 | C.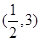 | D.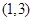 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com