
(本题12分)已知曲线y=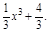
(1)求曲线在x=2处的切线方程;(2)求曲线过点(2,4)的切线方程.
(1)4x-y-4="0." (2)4x-y-4=0或x-y+2=0.
【解析】
试题分析:(1)∵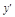 =x2,∴在点P(2,4)处的切线的斜率k=
=x2,∴在点P(2,4)处的切线的斜率k=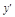 |x=2="4." ……………2分
|x=2="4." ……………2分
∴曲线在点P(2,4)处的切线方程为y-4=4(x-2),即4x-y-4="0." …………………… 4分
(2)设曲线y=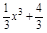 与过点P(2,4)的切线相切于点
与过点P(2,4)的切线相切于点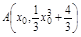 ,
,
则切线的斜率k=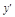 |
|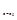 =
=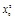 . ……………… 6分
. ……………… 6分
∴切线方程为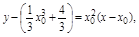 即
即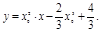 ……………………
8分
……………………
8分
∵点P(2,4)在切线上,∴4=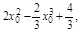
即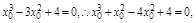 ∴
∴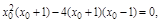
∴(x0+1)(x0-2)2=0,解得x0=-1或x0=2,
故所求的切线方程为4x-y-4=0或x-y+2=0. ……………………12分
考点:本题主要考查导数的几何意义。
点评:易错题,求曲线的切线问题,往往包括两种类型,一是知切点,二是过曲线外的点,后者难度大些。


科目:高中数学 来源:2011年广东省揭阳市第一中学高二上学期期末检测数学理卷 题型:解答题
本题12分)已知 且
且 ,命题P:函数
,命题P:函数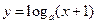 在区间
在区间 上为减函数;命题Q:曲线
上为减函数;命题Q:曲线 与
与 轴相交于不同的两点.若“
轴相交于不同的两点.若“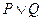 ”为真,“
”为真,“ ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013届云南省高二下学期期中文科数学试卷(解析版) 题型:解答题
(本题12分)已知函数 ,其中
,其中 .
.
(Ⅰ)若曲线 在点
在点 处的切线方程为
处的切线方程为 ,求函数
,求函数 的解析式;
的解析式;
(Ⅱ)讨论函数 的单调性;
的单调性;
(Ⅲ)若对于任意的 ,不等式
,不等式 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013届河北省高二上学期四调理科数学 题型:解答题
(本题满分12分)已知曲线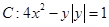
(I)若直线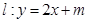 与曲线
与曲线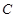 只有一个公共点,求实数
只有一个公共点,求实数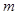 的取值范围;
的取值范围;
(II)若直线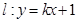 与曲线
与曲线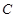 恒有两个不同的交点
恒有两个不同的交点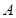 和
和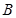 ,且
,且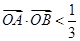 (其中
(其中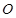 为坐标原点),求实数
为坐标原点),求实数 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com