
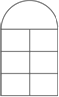
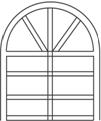
有L米长的钢材,要做成如图所示的窗架,上半部分是半圆,下半部分为6个全等的小长方形组成的长方形,试问小长方形的长、宽为多少时窗户所通过的光线最多?求窗户面积的最大值.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:新课标教材全解高中数学人教A版必修1 人教A版 题型:038
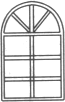
有l米长的钢材,要做成如图所示的窗架,上半部分为半圆,下半部分为六个全等小矩形组成的矩形.试问小矩形的长、宽比为多少时,窗所通过的光线最多,并具体算出窗框面积的最大值.(比值取近似值)
查看答案和解析>>
科目:高中数学 来源:新课标教材全解高中数学人教A版必修1 人教A版 题型:044
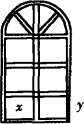
有l(m)长的钢材,要做成(如图所示)的窗架,上半部分为半圆,下半部分为六个全等小矩形组成的矩形.试问小矩形的长、宽比为多少时,窗所通过的光线最多,并具体算出窗框面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
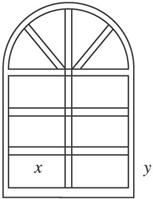
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com