
 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示.若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,并决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,则第4组至少有一名志愿者被抽中的概率为( )
,得到的频率分布直方图如图所示.若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,并决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,则第4组至少有一名志愿者被抽中的概率为( )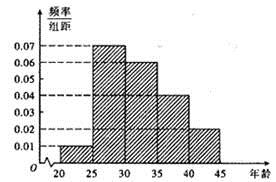
A.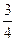 | B. | C. | D. |
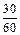 ×6="3;" 第4组:
×6="3;" 第4组: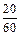 ×6="2;" 第5组:
×6="2;" 第5组: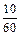 ×6=1.
×6=1.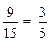 .故选C.
.故选C.

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
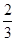 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ,中奖可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率.
,中奖可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com