
(2)已知![]() ,求
,求![]() 的值.
的值.
(3)已知方程sin(α-3π)=2cos(α-4π),求 的值.
的值.
(4)已知tan(π-α)=a2,|cos(π-α)|=-cosα,求![]() 的值.
的值.
思路分析:考查诱导公式和同角三角函数关系式的应用.前三个可以利用诱导公式和同角三角函数关系式将条件和所求的式子化简.而(4)除了化简之外,还应判断角终边的位置.
解:(1)∵sin(3π+α)=sin(π+α)=-sinα,∴sinα=![]() .
.
∴原式=![]() .
.
(2)![]() .
.
(3)∵sin(α-3π)=2cos(α-4π),
∴-sin(3π-α)=2cos(4π-α).
∴-sin(π-α)=2cos(-α).
∴sinα=-2cosα,且cosα≠0.
∴原式=![]() .
.
(4)由题设,tanα=-a2≤0,|cosα|=-cosα,即cosα≤0.
由此,当a≠0时,tanα<0,cosα<0,α为第二象限角,
∴原式=![]() .
.
当a=0时,tanα=0,α=kπ,∴cosα=±1.
∵cosα≤0,∴cosα=-1.
∴原式=![]() (a=0).
(a=0).
综上所述:![]() .
.
方法归纳 三角函数中角的变换是个难点,三角函数中的许多问题正是通过挖掘角与角之间的内在联系而解决的.而化简求值要遵循“负化正,大化小”的原则.
深化升华 本题是一个化简求值的题型,它的特点是已知一个复杂的等式,求另一个复杂的式子的值.解决这类问题的策略是:化简,化简,再化简.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 3 |
| π |
| 2 |
| 3π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| π |
| 2 |
| ||
| 5 |
| π |
| 2 |
| 3π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011年浙江省高一下学期第一次质量检测数学试卷 题型:解答题
(1)已知sin(3π-α)=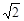 cos(
cos( +β),
+β),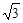 cos(-α)=-
cos(-α)=-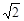 cos(π+β),
cos(π+β),
且0<α<π, 0<β<π,求α, cosβ.
(2)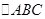 中,
中,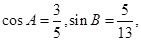 求
求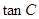
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com