【答案】
分析:结合常见数列的通项形式的不同分别给以总结即可
解答:(1)公式求和法:
①等差数列、等比数列求和公式
②重要公式:1+2+…+n=

n(n+1);
1
2+2
2+…+n
2=

n(n+1)(2n+1);
1
3+2
3+…+n
3=(1+2+…+n)
2=

n
2(n+1)
2;
(2)裂项求和法:将数列的通项分成两个式子的代数和,即a
n=f(n+1)-f(n),然后累加抵消掉中间的许多项,这种先裂后消的求和法叫裂项求和法.用裂项法求和,需要掌握一些常见的裂项,如:a
n=

=
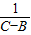
(
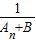
-

);

=
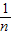
-
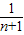
;
(3)错位相减法:对一个由等差数列及等比数列对应项之积组成的数列的前n项和,常用错位相减法.a
n=b
nc
n,其中{b
n}是等差数列,{c
n}是等比数列
(4)倒序相加法:S
n表示从第一项依次到第n项的和,然后又将S
n表示成第n项依次反序到第一项的和,将所得两式相加,由此得到S
n的一种求和方法.
(5)通项分解法(分组求和法):有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等差、等比或常见的数列,然后分别求和,再将其合并即可.a
n=b
n±c
n(6)并项求和法:把数列的某些项放在一起先求和,然后再求S
n.如:100
2-99
2+98
2-97
2+…+2
2-1
2的和.
(7)利用通项求和法:先求出数列的通项,然后进行求和
点评:本题主要考查了常见的数列求和方法的总结,掌握一定的基本方法有利于数列求和问题的求解

 n(n+1);
n(n+1); n(n+1)(2n+1);
n(n+1)(2n+1); n2(n+1)2;
n2(n+1)2; =
=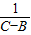 (
(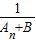 -
- );
); =
=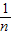 -
-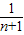 ;
;

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案