
(1)求PQ中点M的轨迹方程.
(2)求|OM|的最小值.
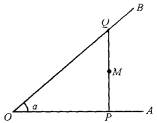
| 解:(1)以O点为原点,OA为x轴正方向,建立直角坐标系,∵P为x轴正半轴
上的一点,设P(x1,0)( x1>0).又点Q在OB上,a 为锐角,设Q( >0, 而S= 即x1= 代入①整理得y2-xytana +4tana =0(x,y∈R*) 即为所求M点的轨迹方程. (2)由所求方程,得x=ycota + ∴ |OM|= = ∵(1+cot2a )y2>0, ∴ y2(1+cot2a )+ ∴ |OM|≥ 当且仅当y2(1+cot2a )=
|


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| OA |
| OB |
| OC |
| 0 |
| A、都是锐角 |
| B、至多有两个钝角 |
| C、恰有两个钝角 |
| D、至少有两个钝角 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市海淀区北师特学校高三(上)第四次月考数学试卷(文科)(解析版) 题型:解答题
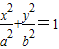 (a>b>0)过点M(0,2),离心率e=
(a>b>0)过点M(0,2),离心率e=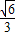 .
.查看答案和解析>>
科目:高中数学 来源:2011年重庆十一中高考数学一模训练试卷(二)(解析版) 题型:选择题
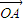 +λ2
+λ2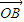 +λ3
+λ3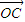 =
=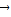 ,则三个角∠AOB、∠BOC、∠COA( )
,则三个角∠AOB、∠BOC、∠COA( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com