
已知:平面α∩平面β=a,平面β∩平面γ=b,平面γ∩平面α=c.
求证:a、b、c相交于同一点或a∥b∥c.
证明:∵α∩β=a,β∩γ=b,∴a、b![]() β.
β.
∴a与b的位置关系只有相交或平行两种情况.
(1)a与b相交时,设a∩b=P,则P∈a,P∈b.
∵a![]() α,b
α,b![]() γ,∴P∈α,P∈γ.
γ,∴P∈α,P∈γ.
∴P为α和γ的公共点.
又∵α∩γ=c,∴P∈c.
∴a、b、c相交于同一点P.
(2)a∥b时,∵α∩γ=c,a![]() α,a
α,a![]() γ,
γ,
∴a∥c.
∴a∥b∥c.
故a、b、c两两平行.
由(1)(2)知a、b、c相交于一点或两两平行.
小结:本题的结论说明三个两两相交的平面,它们的三条交线如果有两条相交于一点,那么这三条相交于一点,如果有两条平行,那么这三条之间互相平行.


科目:高中数学 来源: 题型:044
三个平面两两相交得三条直线,求证这三条直线相交于同一点或两两平行.
已知:平面a∩平面b=a,平面b∩平面γ=6,平面γ∩平面a=c.
求证:a、b、c相交于同一点,或a∥b∥c.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
已知:平面α∩平面β=a,平面β∩平面γ=b,平面γ∩平面α=c.
求证:a、b、c相交于同一点,或a∥b∥c.
查看答案和解析>>
科目:高中数学 来源: 题型:
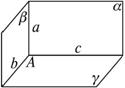
如图,已知平面α、β、γ且α∩β=a,β∩γ=b,γ∩α=C,a∩b=A.求证:A∈C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com