
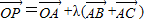 且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;
且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;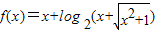 ,则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.
,则“m+n≥0”是“f(m)+f(n)≥0”的充要条件. 进行移项,发现
进行移项,发现 与
与 的关系进行判断;
的关系进行判断;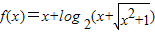 ,证明f(x)是奇函数又是增函数即可证明;
,证明f(x)是奇函数又是增函数即可证明;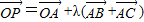 ,
, =λ(
=λ( ),说明p在边BC的中线上,λ∈[0,+∞),
),说明p在边BC的中线上,λ∈[0,+∞),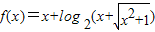 ,f(-x)=-x+
,f(-x)=-x+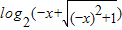
 ]
]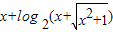 ]=-f(x),f(x)是奇函数,
]=-f(x),f(x)是奇函数,

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| OP |
| OA |
| AB |
| AC |
| g | 2 |
| x2+1 |
查看答案和解析>>
科目:高中数学 来源:河北省正定中学2010届高三上学期期中考试数学理科试题 题型:022
下列说法中:①函数y=lg(x2-ax-a)的值域为R,则a∈(-4,0);
②O是△ABC所在平面上一定点,动点P满足![]() 且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;
且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;
③要得到函数y=f(1-x)的图象只需将y=f(-x)的图像向左平移1个单位;
④若函数f(x)=x+log2(x+![]() ),则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.其中正确的序号是________.
),则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.其中正确的序号是________.
查看答案和解析>>
科目:高中数学 来源:河北省正定中学2010届高三上学期期中考试数学文科试题 题型:022
下列说法中:①函数y=lg(x2-ax-a)的值域为R,则a∈(-4,0);
②O是△ABC所在平面上一定点,动点P满足![]() 且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;
且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;
③要得到函数y=f(1-x)的图象只需将y=f(-x)的图像向左平移1个单位;
④若函数f(x)=x+log2(x+![]() ),则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.其中正确的序号是________.
),则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.其中正确的序号是________.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省临沂市映达高考补习学校高三一轮复习期中迎考数学模拟试卷1(理科)(解析版) 题型:填空题
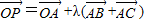 且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;
且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;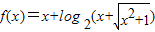 ,则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.
,则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com