
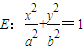 (a>b>0)的一个公共点为B(0,2).F为椭圆E的右焦点,直线BF与圆C相切于点B.
(a>b>0)的一个公共点为B(0,2).F为椭圆E的右焦点,直线BF与圆C相切于点B.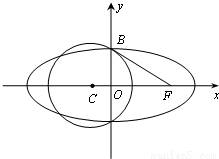
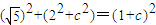 ,从而可求c=4,利用a2=b2+c2,b=2,可得a2=20,从而可求椭圆E的方程;
,从而可求c=4,利用a2=b2+c2,b=2,可得a2=20,从而可求椭圆E的方程;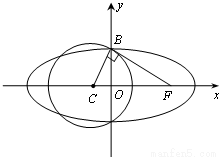 解:(Ⅰ)由题可知,b=2…(1分)
解:(Ⅰ)由题可知,b=2…(1分)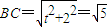 ,∴t=±1,又t>0,∴t=1…(3分)
,∴t=±1,又t>0,∴t=1…(3分)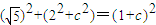 ,∴c=4,…(5分)
,∴c=4,…(5分)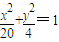 …(6分)
…(6分)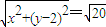 ,即x2+(y-2)2=20…②
,即x2+(y-2)2=20…② ,∴M(-2,-2)…(9分)
,∴M(-2,-2)…(9分)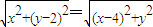 ,即2x-y=3…③
,即2x-y=3…③ ,∴M(1,-1)…(11分)
,∴M(1,-1)…(11分)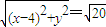 ,即x2+y2-8x-4=0…④
,即x2+y2-8x-4=0…④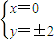 ,又B(0,2),∴M(0,-2)…(13分)
,又B(0,2),∴M(0,-2)…(13分)

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
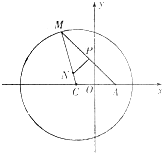 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足AM=2AP,NP⊥AM,点N的轨迹为曲线E.
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足AM=2AP,NP⊥AM,点N的轨迹为曲线E.| 1 |
| 2 |
| ||
| 2 |
| y | 2 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x°2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
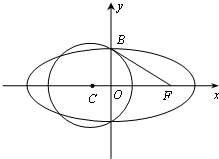 (2010•深圳二模)已知圆C:(x+t)2+y2=5(t>0)和椭圆E:
(2010•深圳二模)已知圆C:(x+t)2+y2=5(t>0)和椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com