
 的等腰三角形,则该三棱锥的外接球体积为
的等腰三角形,则该三棱锥的外接球体积为 

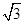
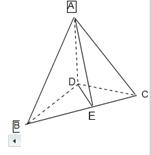
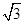 ,0),∵(x-2)2+y2+z2=x2+y2+z2,①x2+y2+(z-2)2=x2+y2+z2,②(x+1)2+(y-
,0),∵(x-2)2+y2+z2=x2+y2+z2,①x2+y2+(z-2)2=x2+y2+z2,②(x+1)2+(y-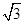 )2+z2=x2+y2+z2,③∴x=1,y=
)2+z2=x2+y2+z2,③∴x=1,y=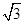 ,z=1,∴球心的坐标是(1,
,z=1,∴球心的坐标是(1,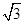 ,1),所以球的半径是
,1),所以球的半径是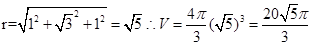


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com