
【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,大学生
推出的多款健康运动软件中的一款,大学生![]() 的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:
的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:![]() 、0~2000步,(说明:“0~2000”表示“大于或等于0,小于2000”,以下同理),
、0~2000步,(说明:“0~2000”表示“大于或等于0,小于2000”,以下同理),![]() 、2000~5000步,
、2000~5000步,![]() 、5000~8000步,
、5000~8000步,![]() 、8000~10000步,
、8000~10000步,![]() 、10000~12000步,且
、10000~12000步,且![]() 三种类别的人数比例为
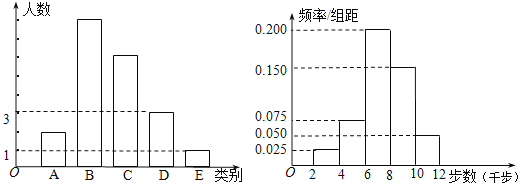
三种类别的人数比例为![]() ,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.
,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.
参与者 | 超越者 | 合计 | |
男 | 20 | ||
女 | 20 | ||
合计 | 40 |
若某人一天的走路步数大于或等于8000,则被系统认定为“超越者”,否则被系统认定为“参与者”.
(Ⅰ)若以大学生![]() 抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生
抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生![]() 的参与“微信运动”的400位微信好友中,每天走路步数在
的参与“微信运动”的400位微信好友中,每天走路步数在
(Ⅱ)若在大学生![]() 该天抽取的步数在8000~12000的微信好友中,按男女比例分层抽取9人进行身体状况调查,然后再从这9位微信好友中随机抽取4人进行采访,求其中至少有一位女性微信好友被采访的概率;
该天抽取的步数在8000~12000的微信好友中,按男女比例分层抽取9人进行身体状况调查,然后再从这9位微信好友中随机抽取4人进行采访,求其中至少有一位女性微信好友被采访的概率;
(Ⅲ)请根据抽取的样本数据完成下面的![]() 列联表,并据此判断能否有
列联表,并据此判断能否有![]() 的把握认为“认定类别”与“性别”有关?
的把握认为“认定类别”与“性别”有关?
【答案】(Ⅰ)260; (Ⅱ)![]() ; (Ⅲ)见解析.
; (Ⅲ)见解析.
【解析】
(Ⅰ)所抽取的40人中,该天行走2000~8000步的人数:男12人,女14人,400位参与“微信运动”的微信好友中,每天行走2000~8000步的人数约为:![]() 人;
人;
(Ⅱ)根据分层抽样可得男6人,女3人,再根据古典概型的概率公式可得;
(Ⅲ)根据列联表计算出![]() 的观测值,结合临界值表可得.
的观测值,结合临界值表可得.
(Ⅰ)所抽取的40人中,该天行走2000~8000步的人数:男12人,
女14人,400位参与“微信运动”的微信好友中,每天行走2000~8000步的人数
约为:![]() 人;
人;
(Ⅱ)该天抽取的步数在8000~12000的人数:男8人,女4人,
再按男女比例分层抽取9人,则其中男6人,女3人
所求概率![]() (或
(或![]() )
)
(Ⅲ)完成![]() 列联表
列联表
参与者 | 超越者 | 合计 | |
男 | 12 | 8 | 20 |
女 | 16 | 4 | 20 |
合计 | 28 | 12 | 40 |
计算![]() ,
,
因为![]() ,所以没有理由认为“认定类别”与“性别”有关,
,所以没有理由认为“认定类别”与“性别”有关,
即“认定类别”与“性别”无关


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为 ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与曲线
与曲线![]() 两交点所在直线的极坐标方程;
两交点所在直线的极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() ,以极点
,以极点![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴非负半轴建立平面直角坐标系.
轴非负半轴建立平面直角坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 是曲线
是曲线![]() 上一动点,过点
上一动点,过点![]() 作线段
作线段![]() 的垂线交曲线
的垂线交曲线![]() 于点
于点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某茶楼有四类茶饮,假设为顾客准备泡茶工具所需的时间互相独立,且都是整数分钟,经统计以往为100位顾客准备泡茶工具所需的时间![]() ,结果如下:
,结果如下:
类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
顾客数(人) | 20 | 30 | 40 | 10 |
时间 | 2 | 3 | 4 | 6 |
注:服务员在准备泡茶工具时的间隔时间忽略不计,并将频率视为概率.
(1)求服务员恰好在第6分种开始准备第三位顾客的泡茶工具的概率;
(2)用![]() 表示至第4分钟末已准备好了工具的顾客人数,求
表示至第4分钟末已准备好了工具的顾客人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x-![]() (a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(1)若对[1,+![]() )内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
)内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
(2)当a=l时,求最大的正整数k,使得对[e,3](e=2.71828是自然对数的底数)内的任意k个实数x1,x2,,xk都有![]() 成立;
成立;
(3)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( ).
①在![]() 中,若
中,若![]() ,则
,则![]() 是等腰三角形;
是等腰三角形;
②在![]() 中,若
中,若 ![]() ,则
,则![]()
③两个向量![]() ,
,![]() 共线的充要条件是存在实数
共线的充要条件是存在实数![]() ,使
,使![]()
④等差数列的前![]() 项和公式是常数项为0的二次函数.
项和公式是常数项为0的二次函数.
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com