
分析 根据题意和偶函数的单调性关系,判断出f(x)在[0,3]上的单调性,利用偶函数的性质转化不等式,由函数的单调性和定义域列出不等式组,求出实数m的取值范围.
解答 解:∵f(x)是定义在[-3,3]上的偶函数,且在[-3,0]上是增函数,
∴函数f(x)在[0,3]上是减函数,
由f(1-2m)<f(m)得,f(|1-2m|)<f(|m|),
∴$\left\{\begin{array}{l}{-3≤1-2m≤3}\\{-3≤m≤3}\\{|1-2m|>|m|}\end{array}\right.$,解得$-1≤m<\frac{1}{3}$或1<m≤2,
所以实数m的取值范围是$[-1,\frac{1}{3})∪(1,2]$,
故答案为:$[-1,\frac{1}{3})∪(1,2]$.
点评 本题考查了偶函数的性质,函数的奇偶性与单调性的综合应用,考查转化思想,注意函数的定义域,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ①③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=$\frac{4}{n(n+1)}$ | B. | an=$\frac{2}{n+1}$ | C. | an=$\frac{4}{n+1}$ | D. | an=$\frac{2}{{n}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+4x+4>0 | B. | |x|>0 | C. | x2-x+1≥0 | D. | $\frac{1}{x}$-1<$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
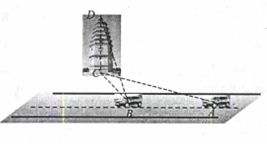 一辆汽车在一条水平的公路上向正西行驶,如图,到A处时测得公路北侧一铁塔底部C在西偏北30°的方向上,行驶200m后到达B处,测得此铁塔底部C在西偏北75°的方向上,塔顶D的仰角为30°,则此铁塔的高度为( )
一辆汽车在一条水平的公路上向正西行驶,如图,到A处时测得公路北侧一铁塔底部C在西偏北30°的方向上,行驶200m后到达B处,测得此铁塔底部C在西偏北75°的方向上,塔顶D的仰角为30°,则此铁塔的高度为( )| A. | $\frac{100\sqrt{6}}{3}$m | B. | 50$\sqrt{6}$m | C. | 100$\sqrt{3}$m | D. | 100$\sqrt{2}$m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com