
在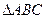 三角形ABC中,已知内角A、B、C所对的边分别为a、b、c,已知
三角形ABC中,已知内角A、B、C所对的边分别为a、b、c,已知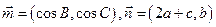 且
且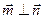
(1)求角B的大小及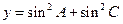 的取值范围;
的取值范围;
(2)若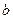 =
=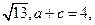 求
求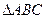 的面积.
的面积.
解 (1)由余弦定理得COS B=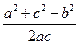 ,cos C=
,cos C=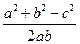 ,将上式代入(2
,将上式代入(2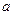 +c)cos B+bcos C=0,整理得
+c)cos B+bcos C=0,整理得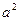 +
+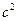 -
-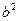 =-
=-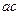 ,
,
∴cos B=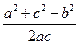 =
=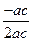 =-
=-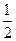 ,
,
∵角B为三角形的内角,∴B=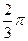 ,
,
由题知,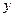 =sin2A+sin2 C=
=sin2A+sin2 C=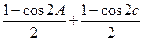 =1-
=1-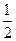 (cos2A+cos2C).
(cos2A+cos2C).
由A+C=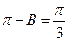 ,得C=
,得C=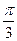 -A,
-A,
∵cos2A+cos2C=cos2A+cos(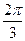 -2A)=
-2A)= 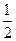 cos2A+
cos2A+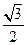 sin2A=sin(2A+
sin2A=sin(2A+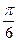 ),
),
由于0<A<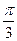 ,故
,故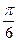 <2A+
<2A+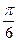 <
<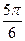 ,
,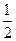 <sin(2A+
<sin(2A+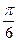 )≤1,-
)≤1,- 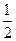 ≤-
≤-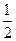 sin(2A+
sin(2A+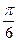 )<-
)<-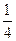 ,
,
所以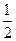 ≤1-
≤1-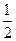 sin(2A+
sin(2A+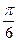 )<
)<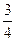 ,故
,故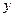 的取值范围是[
的取值范围是[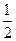 ,
,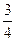 ].
].
(2)将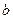 =
=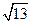 ,
,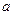 +
+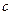 =4,B=
=4,B=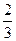
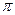 代入
代入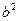 =
=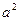 +
+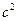 -2
-2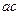 cosB即
cosB即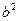 =(
=(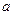 +
+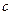 )2-2
)2-2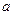
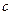 -2
-2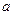
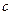 cosB,
cosB,
∴13=16-2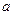
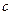 (1-
(1-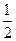 ),∴
),∴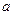
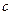 =3,
=3,
∴△ABC的面积为S△ABC=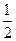
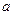
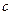 sin B=
sin B=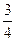
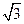 .
.
解析


科目:高中数学 来源: 题型:
| AB |
| AC |
| AB |
| AC |
4
| ||
| 7 |
| π |
| 3 |
| 5π |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com