
【题目】已知函数f(x)=|sinx|+cosx,现有如下几个命题: ①该函数为偶函数;
②该函数最小正周期为 ![]() ;
;
③该函数值域为 ![]() ;
;
④若定义区间(a,b)的长度为b﹣a,则该函数单调递增区间长度的最大值为 ![]() .
.
其中正确命题为 .
【答案】①③④
【解析】解:当sinx≥0,即2kπ≤x≤2kπ+π,k∈Z,此时f(x)=sinx+cosx= ![]() sin(x+
sin(x+ ![]() ), 当sinx<0,即2kπ﹣π≤x≤2kπ,k∈Z,此时f(x)=﹣sinx+cosx=
), 当sinx<0,即2kπ﹣π≤x≤2kπ,k∈Z,此时f(x)=﹣sinx+cosx= ![]() cos(x+
cos(x+ ![]() ),①f(﹣x)=|sin(﹣x)|+cosx=|sinx|+cosx=f(x),则函数f(x)是偶函数,故①正确,②f(x+
),①f(﹣x)=|sin(﹣x)|+cosx=|sinx|+cosx=f(x),则函数f(x)是偶函数,故①正确,②f(x+ ![]() )=|sin(x+
)=|sin(x+ ![]() )|+cos(x+
)|+cos(x+ ![]() )=|cosx|﹣sinx≠f(x),则函数最小正周期为
)=|cosx|﹣sinx≠f(x),则函数最小正周期为 ![]() 错误,故②错误,
错误,故②错误,
当2kπ≤x≤2kπ+π时,2kπ+ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,此时
,此时 ![]() sin(x+
sin(x+ ![]() )∈[﹣1,
)∈[﹣1, ![]() ],
],
当2kπ﹣π≤x≤2kπ时,2kπ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,此时
,此时 ![]() cos(x+
cos(x+ ![]() )∈[﹣1,
)∈[﹣1, ![]() ],
],
综上f(x))∈[﹣1, ![]() ],即函数的值域为[﹣1,
],即函数的值域为[﹣1, ![]() ],故③正确,④作出函数f(x)的图象如图:
],故③正确,④作出函数f(x)的图象如图: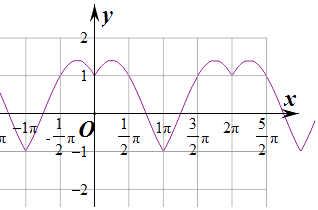
函数单调递增的最大区间在函数f(x)= ![]() cos(x+
cos(x+ ![]() ),
),
由2kπ﹣π≤x+ ![]() ≤2kπ,k∈Z得2kπ﹣
≤2kπ,k∈Z得2kπ﹣ ![]() ≤x≤2kπ﹣
≤x≤2kπ﹣ ![]() ,k∈Z
,k∈Z
∵2kπ﹣π≤x≤2kπ,∴此时2kπ﹣π≤x≤2kπ﹣ ![]() ,即此时函数的单调递增区间为[2kπ﹣π,2kπ﹣
,即此时函数的单调递增区间为[2kπ﹣π,2kπ﹣ ![]() ],
],
当k=0时,单调递增区间为[﹣π,﹣ ![]() ],此时区间长度为﹣
],此时区间长度为﹣ ![]() ﹣(﹣π)=
﹣(﹣π)= ![]() ,
,
故④正确,
所以答案是:①③④.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】等差数列{an}前n项和为Sn , 且S5=45,S6=60.
(1)求{an}的通项公式an;
(2)若数列{an}满足bn+1﹣bn=an(n∈N*)且b1=3,求{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x3+1+a( ![]() ≤x≤e,e是自然对数的底)与g(x)=3lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
≤x≤e,e是自然对数的底)与g(x)=3lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
A.[0,e3﹣4]
B.[0, ![]() +2]
+2]
C.[ ![]() +2,e3﹣4]
+2,e3﹣4]
D.[e3﹣4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠DAB= ![]() ,AC∩BD=O,且PO⊥平面ABCD,PO=
,AC∩BD=O,且PO⊥平面ABCD,PO= ![]() ,点F,G分别是线段PB,PD上的中点,E在PA上,且PA=3PE.
,点F,G分别是线段PB,PD上的中点,E在PA上,且PA=3PE. 
(Ⅰ)求证:BD∥平面EFG;
(Ⅱ)求直线AB与平面EFG的成角的正弦值;
(Ⅲ)请画出平面EFG与四棱锥的表面的交线,并写出作图的步骤.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=2,a4=14,数列{bn}满足b1=1,b4=6,且{an﹣bn}是等比数列. (Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)若n∈N* , 都有bn≤bk成立,求正整数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆W: ![]() (b>0)的一个焦点坐标为
(b>0)的一个焦点坐标为 ![]() .
.
(Ⅰ)求椭圆W的方程和离心率;
(Ⅱ)若椭圆W与y轴交于A,B两点(A点在B点的上方),M是椭圆上异于A,B的任意一点,过点M作MN⊥y轴于N,E为线段MN的中点,直线AE与直线y=﹣1交于点C,G为线段BC的中点,O为坐标原点.求∠OEG的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数 ![]() 在(0,2)上存在两个极值点,则a的取值范围是( )
在(0,2)上存在两个极值点,则a的取值范围是( )
A.(﹣∞,﹣ ![]() )
)
B.(﹣∞,﹣ ![]() )
)
C.(﹣∞,﹣ ![]() )∪(﹣
)∪(﹣ ![]() ,﹣
,﹣ ![]() )
)
D.(﹣e,﹣ ![]() )∪(1,+∞)
)∪(1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com