
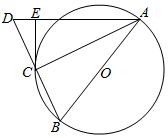
 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2.
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2.分析 (1)利用AB是圆O的直径,可得∠ACB=90°.即AC⊥BD.又已知BC=CD,可得△ABD是等腰三角形,可得∠D=∠B.再利用弦切角定理可得∠ACE=∠B,得到∠AEC=∠ACB=90°,即可得出结论;
(2)由(1)可知△AEC∽△ACB,即可求AC的长.
解答 (1)证明:∵AB是圆O的直径,∴∠ACB=90°.即AC⊥BD.
又∵BC=CD,∴AB=AD,∴∠D=∠ABC,∠EAC=∠BAC.
∵CE与⊙O相切于点C,∴∠ACE=∠ABC.∴∠AEC=∠ACB=90°.
∴CE⊥AD;
(2)解:由(1)可知△AEC∽△ACB,
∴$\frac{AE}{AC}$=$\frac{AC}{AB}$,
∴AC2=AE•AB=(6-2)×6=24,
∴AC=2$\sqrt{6}$.
点评 本题综合考查了圆的性质、弦切角定理、等腰三角形的性质、相似三角形的判定与性质等基础知识,需要较强的推理能力.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{e_1}=(0,1),\overrightarrow{e_2}=(0,-2)$ | B. | $\overrightarrow{e_1}=(1,5),\overrightarrow{e_2}=(-2,-10)$ | ||
| C. | $\overrightarrow{e_1}=(-5,3),\overrightarrow{e_2}=(-2,1)$ | D. | $\overrightarrow{e_1}=(7,8),\overrightarrow{e_2}=(-7,-8)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若p,则q”与命题“若¬q,则¬p”互为逆否命题 | |
| B. | 命题p:“?x∈[0,1],1≤ex≤e”(e是自然对数的底数),命题q:“?x∈R,x2+x+1<0”,则p∨q为真 | |
| C. | “am2<bm2”是“a<b”成立的必要不充分条件 | |
| D. | 若p∨q为假命题,则p、q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5+2$\sqrt{2}$ | B. | 2 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | [1,+∞) | C. | [-1,+∞) | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | -15 | C. | 135 | D. | -135 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com