
ΓΨΧβΡΩΓΩΡ≥≥§ –¥”2014ΡξΦΉΓΔ““ΝΫ÷÷ΥαΡΧΒΡ»’œζ έΝΩΘ®ΒΞΈΜΘΚœδΘ©ΒΡ ΐΨί÷–Ζ÷±πΥφΜζ≥ι»Γ100ΗωΘ§≤ΔΑ¥[ 0Θ§10]Θ§Θ®10Θ§20]Θ§Θ®20Θ§30]Θ§Θ®30Θ§40]Θ§Θ®40Θ§50]Ζ÷ΉιΘ§ΒΟΒΫΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γœ¬ΘΚ
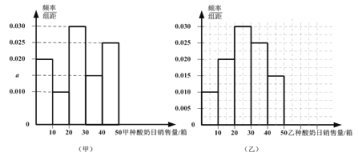
ΦΌ…ηΦΉΓΔ““ΝΫ÷÷ΥαΡΧΕάΝΔœζ έ«“»’œζ έΝΩœύΜΞΕάΝΔΘ°
Θ®1Θ©–¥≥ωΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ®ΦΉΘ©÷–ΒΡ![]() ΒΡ÷ΒΘΜΦ«ΦΉ÷÷ΥαΡΧ”κ““÷÷ΥαΡΧ»’œζ έΝΩΘ®ΒΞΈΜΘΚœδΘ©ΒΡΖΫ≤νΖ÷±πΈΣ
ΒΡ÷ΒΘΜΦ«ΦΉ÷÷ΥαΡΧ”κ““÷÷ΥαΡΧ»’œζ έΝΩΘ®ΒΞΈΜΘΚœδΘ©ΒΡΖΫ≤νΖ÷±πΈΣ![]() Θ§
Θ§![]() Θ§ ‘±»Ϋœ
Θ§ ‘±»Ϋœ![]() ”κ
”κ![]() ΒΡ¥σ–ΓΘΜΘ®÷Μ–η–¥≥ωΫα¬έΘ©
ΒΡ¥σ–ΓΘΜΘ®÷Μ–η–¥≥ωΫα¬έΘ©
Θ®2Θ©ΙάΦΤ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§ΦΉΓΔ““ΝΫ÷÷ΥαΡΧΒΡœζ έΝΩ«Γ”–“ΜΗωΗΏ”Ύ20œδ«“Νμ“ΜΗω≤ΜΗΏ”Ύ20œδΒΡΗ≈¬ ΘΜ
Θ®3Θ©…η![]() ±μ Ψ‘ΎΈ¥ά¥3ΧλΡΎΦΉ÷÷ΥαΡΧΒΡ»’œζ έΝΩ≤ΜΗΏ”Ύ20œδΒΡΧλ ΐΘ§“‘»’œζ έΝΩ¬δ»κΗςΉιΒΡΤΒ¬ ΉςΈΣΗ≈¬ Θ§«σ
±μ Ψ‘ΎΈ¥ά¥3ΧλΡΎΦΉ÷÷ΥαΡΧΒΡ»’œζ έΝΩ≤ΜΗΏ”Ύ20œδΒΡΧλ ΐΘ§“‘»’œζ έΝΩ¬δ»κΗςΉιΒΡΤΒ¬ ΉςΈΣΗ≈¬ Θ§«σ![]() ΒΡ ΐ―ßΤΎΆϊΘ°
ΒΡ ΐ―ßΤΎΆϊΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§![]() ΘΜΘ®2Θ©0Θ°42ΘΜΘ®3Θ©0Θ°9Θ°
ΘΜΘ®2Θ©0Θ°42ΘΜΘ®3Θ©0Θ°9Θ°
ΓΨΫβΈωΓΩ
‘ΧβΘ®ΔώΘ©”…ΗςΗω–ΓΨΊ–ΈΒΡΟφΜΐΚΆΈΣ1Θ§œ»«σ≥ω![]() Θ§”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΩ…Ω¥≥ωΘ§ΦΉΒΡœζ έΝΩ±»ΫœΖ÷…ΔΘ§Εχ““ΫœΈΣΦ·÷–Θ§”…¥ΥΩ…ΒΟ≥ω
Θ§”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΩ…Ω¥≥ωΘ§ΦΉΒΡœζ έΝΩ±»ΫœΖ÷…ΔΘ§Εχ““ΫœΈΣΦ·÷–Θ§”…¥ΥΩ…ΒΟ≥ω![]() ”κ
”κ![]() ΒΡ¥σ–ΓΙΊœΒΘΜΘ®ΔρΘ© Ήœ»…η ¬Φΰ
ΒΡ¥σ–ΓΙΊœΒΘΜΘ®ΔρΘ© Ήœ»…η ¬Φΰ![]() ΘΚ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§ΦΉ÷÷ΥαΡΧΒΡœζ έΝΩ≤ΜΗΏ”Ύ20œδΘΜ ¬Φΰ
ΘΚ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§ΦΉ÷÷ΥαΡΧΒΡœζ έΝΩ≤ΜΗΏ”Ύ20œδΘΜ ¬Φΰ![]() ΘΚ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§““÷÷ΥαΡΧΒΡœζ έΝΩ≤ΜΗΏ”Ύ20œδΘΜ ¬Φΰ
ΘΚ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§““÷÷ΥαΡΧΒΡœζ έΝΩ≤ΜΗΏ”Ύ20œδΘΜ ¬Φΰ![]() ΘΚ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§ΦΉΓΔ““ΝΫ÷÷ΥαΡΧΒΡœζ έΝΩ«ΓΚΟ“ΜΗωΗΏ”Ύ20œδ«“Νμ“ΜΗω≤ΜΗΏ”Ύ20œδΘΜ»ΜΚσΖ÷±π«σ≥ω ¬Φΰ
ΘΚ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§ΦΉΓΔ““ΝΫ÷÷ΥαΡΧΒΡœζ έΝΩ«ΓΚΟ“ΜΗωΗΏ”Ύ20œδ«“Νμ“ΜΗω≤ΜΗΏ”Ύ20œδΘΜ»ΜΚσΖ÷±π«σ≥ω ¬Φΰ![]() ΚΆ ¬Φΰ
ΚΆ ¬Φΰ![]() ΒΡΗ≈¬ Θ§ΉνΚσ”…œύΜΞΕάΝΔ ¬ΦΰΒΡΗ≈¬ ≥ΥΖ®ΦΤΥψΙΪ ΫΦ¥Ω…ΒΟ≥ωΥυ«σΒΡΫαΙϊΘΜΘ®ΔσΘ© Ήœ»”…Χβ“βΩ…÷Σ
ΒΡΗ≈¬ Θ§ΉνΚσ”…œύΜΞΕάΝΔ ¬ΦΰΒΡΗ≈¬ ≥ΥΖ®ΦΤΥψΙΪ ΫΦ¥Ω…ΒΟ≥ωΥυ«σΒΡΫαΙϊΘΜΘ®ΔσΘ© Ήœ»”…Χβ“βΩ…÷Σ![]() ΒΡΩ…Ρή»Γ÷ΒΈΣ0Θ§1Θ§2Θ§3Θ§»ΜΚσ‘Υ”ΟœύΜΞΕάΝΔ÷ΊΗ¥ ‘―ιΒΡΗ≈¬ ΦΤΥψΙΪ ΫΖ÷±πΦΤΥψœύ”ΠΒΡΗ≈¬ Θ§ΉνΚσΒΟ≥ωΤδΖ÷≤ΦΝ–Φ¥Ω…Θ°
ΒΡΩ…Ρή»Γ÷ΒΈΣ0Θ§1Θ§2Θ§3Θ§»ΜΚσ‘Υ”ΟœύΜΞΕάΝΔ÷ΊΗ¥ ‘―ιΒΡΗ≈¬ ΦΤΥψΙΪ ΫΖ÷±πΦΤΥψœύ”ΠΒΡΗ≈¬ Θ§ΉνΚσΒΟ≥ωΤδΖ÷≤ΦΝ–Φ¥Ω…Θ°
‘ΧβΫβΈωΘΚΘ®ΔώΘ©”…Ης–ΓΨΊ–ΈΒΡΟφΜΐΚΆΈΣ1Ω…ΒΟΘΚ![]() Θ§Ϋβ÷°ΒΡ
Θ§Ϋβ÷°ΒΡ
![]() ΘΜ”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΩ…Ω¥≥ωΘ§ΦΉΒΡœζ έΝΩ±»ΫœΖ÷…ΔΘ§Εχ““ΫœΈΣΦ·÷–Θ§÷ς“ΣΦ·÷–‘Ύ
ΘΜ”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΩ…Ω¥≥ωΘ§ΦΉΒΡœζ έΝΩ±»ΫœΖ÷…ΔΘ§Εχ““ΫœΈΣΦ·÷–Θ§÷ς“ΣΦ·÷–‘Ύ![]() œδΘ§Ι
œδΘ§Ι
![]() Θ°
Θ°
Θ®ΔρΘ©…η ¬Φΰ![]() ΘΚ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§ΦΉ÷÷ΥαΡΧΒΡœζ έΝΩ≤ΜΗΏ”Ύ20œδΘΜ ¬Φΰ
ΘΚ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§ΦΉ÷÷ΥαΡΧΒΡœζ έΝΩ≤ΜΗΏ”Ύ20œδΘΜ ¬Φΰ![]() ΘΚ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§““÷÷ΥαΡΧΒΡœζ έΝΩ≤ΜΗΏ”Ύ20œδΘΜ ¬Φΰ
ΘΚ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§““÷÷ΥαΡΧΒΡœζ έΝΩ≤ΜΗΏ”Ύ20œδΘΜ ¬Φΰ![]() ΘΚ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§ΦΉΓΔ““ΝΫ÷÷ΥαΡΧΒΡœζ έΝΩ«ΓΚΟ“ΜΗωΗΏ”Ύ20œδ«“Νμ“ΜΗω≤ΜΗΏ”Ύ20œδΘ°‘ρ
ΘΚ‘ΎΈ¥ά¥ΒΡΡ≥“ΜΧλάοΘ§ΦΉΓΔ““ΝΫ÷÷ΥαΡΧΒΡœζ έΝΩ«ΓΚΟ“ΜΗωΗΏ”Ύ20œδ«“Νμ“ΜΗω≤ΜΗΏ”Ύ20œδΘ°‘ρ![]() Θ§
Θ§![]() Θ°Υυ“‘
Θ°Υυ“‘![]() Θ°
Θ°
Θ®ΔσΘ©”…Χβ“βΩ…÷ΣΘ§![]() ΒΡΩ…Ρή»Γ÷ΒΈΣ0Θ§1Θ§2Θ§3Θ°
ΒΡΩ…Ρή»Γ÷ΒΈΣ0Θ§1Θ§2Θ§3Θ°
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ°
Θ°
Υυ“‘![]() ΒΡΖ÷≤ΦΝ–ΈΣ
ΒΡΖ÷≤ΦΝ–ΈΣ
| 0 | 1 | 2 | 3 |
| 0Θ°343 | 0Θ°441 | 0Θ°189 | 0Θ°027 |
Υυ“‘![]() ΒΡ ΐ―ßΤΎΆϊ
ΒΡ ΐ―ßΤΎΆϊ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏ![]() ΒΡΫΙΒψΈΣ
ΒΡΫΙΒψΈΣ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ”κ
”κ![]() ÷αΒΡΫΜΒψΈΣ
÷αΒΡΫΜΒψΈΣ![]() Θ§”κ
Θ§”κ![]() ΒΡΫΜΒψΈΣ
ΒΡΫΜΒψΈΣ![]() Θ§«“
Θ§«“![]() Θ°
Θ°
Θ®ΔώΘ©«σ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©…ηΙΐΕ®Βψ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ”κ≈ΉΈοœΏ
”κ≈ΉΈοœΏ![]() ΫΜ”Ύ
ΫΜ”Ύ![]() Θ§
Θ§![]() ΝΫΒψΘ§Ν§Ϋ”
ΝΫΒψΘ§Ν§Ϋ”![]() ≤Δ―”≥ΛΫΜ≈ΉΈοœΏΒΡΉΦœΏ”ΎΒψ
≤Δ―”≥ΛΫΜ≈ΉΈοœΏΒΡΉΦœΏ”ΎΒψ![]() Θ§Β±÷±œΏ
Θ§Β±÷±œΏ![]() «Γ”κ≈ΉΈοœΏœύ«– ±Θ§«σ÷±œΏ
«Γ”κ≈ΉΈοœΏœύ«– ±Θ§«σ÷±œΏ![]() ΒΡΖΫ≥ΧΘ°
ΒΡΖΫ≥ΧΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐf(x)ΘΫ4cos ΠΊxΓΛsin![]() ΘΪa(ΠΊ>0)ΆΦœσ…œΉνΗΏΒψΒΡΉίΉχ±ξΈΣ2Θ§«“ΆΦœσ…œœύΝΎΝΫΗωΉνΗΏΒψΒΡΨύάκΈΣΠ–.
ΘΪa(ΠΊ>0)ΆΦœσ…œΉνΗΏΒψΒΡΉίΉχ±ξΈΣ2Θ§«“ΆΦœσ…œœύΝΎΝΫΗωΉνΗΏΒψΒΡΨύάκΈΣΠ–.
(1)«σaΚΆΠΊΒΡ÷ΒΘΜ
(2)«σΚ· ΐf(x)‘Ύ[0Θ§Π–]…œΒΡΒΞΒςΒίΦθ«χΦδ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣaΓ RΘ§ΟϋΧβpΘΚΓΑxΓ [1Θ§2]Θ§x2©¹aΓί0Γ±Θ§ΟϋΧβqΘΚΓΑxΓ RΘ§x2+2ax+2©¹a=0Γ±Θ°
Θ®1Θ©»τΟϋΧβpΈΣ’φΟϋΧβΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©»τΟϋΧβΓΑpΓ≈qΓ±ΈΣ’φΟϋΧβΘ§ΟϋΧβΓΑpΓΡqΓ±ΈΣΦΌΟϋΧβΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©ΘΫex+ax2+bxΘ®eΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉΘ§aΘ§bΈΣ≥Θ ΐΘ©Θ§«ζœΏyΘΫfΘ®xΘ©‘ΎxΘΫ0¥ΠΒΡ«–œΏΨ≠ΙΐΒψAΘ®©¹1Θ§©¹1Θ©
Θ®1Θ©«σ Β ΐbΒΡ÷ΒΘΜ
Θ®2Θ© «Ζώ¥φ‘Ύ Β ΐaΘ§ ΙΒΟ«ζœΏyΘΫfΘ®xΘ©Υυ”–«–œΏΒΡ–±¬ ΕΦ≤Μ–Γ”Ύ2ΘΩ»τ¥φ‘ΎΘ§«σ Β ΐaΒΡ»Γ÷ΒΦ·ΚœΘ§»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®1Θ©»τΙΊ”ΎxΒΡ≤ΜΒ» Ϋax2©¹3x+2ΘΨ0Θ®aΓ RΘ©ΒΡΫβΦ·ΈΣ{x|xΘΦ1ΜρxΘΨb}Θ§«σaΘ§bΒΡ÷ΒΘΜ
Θ®2Θ©ΫβΙΊ”ΎxΒΡ≤ΜΒ» Ϋax2©¹3x+2ΘΨ5©¹axΘ®aΓ RΘ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ –Ά≥ΦΤΨ÷ΨΆΡ≥ΒΊΨ”ΟώΒΡ‘¬ ’»κΒς≤ιΝΥ10000»ΥΘ§≤ΔΗυΨίΥυΒΟ ΐΨίΜ≠≥ω―υ±ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ®ΟΩΗωΖ÷ΉιΑϋά®ΉσΕΥΒψΘ§≤ΜΑϋά®”“ΕΥΒψΘ§»γΒΎ“ΜΉι±μ Ψ ’»κ‘Ύ![]() Θ©.
Θ©.
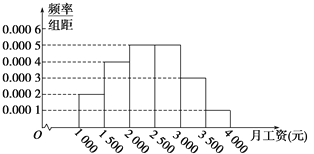
Θ®1Θ©«σΨ”Οώ ’»κ‘Ύ![]() ΒΡΤΒ¬ ΘΜ
ΒΡΤΒ¬ ΘΜ
Θ®2Θ©ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΥψ≥ω―υ±Ψ ΐΨίΒΡ÷–ΈΜ ΐΘΜ
Θ®3Θ©ΈΣΝΥΖ÷ΈωΨ”ΟώΒΡ ’»κ”κΡξΝδΓΔ÷Α“ΒΒ»ΖΫΟφΒΡΙΊœΒΘ§±Ί–κΑ¥‘¬ ’»κ‘Ό¥”’β10000»Υ÷–Α¥Ζ÷≤ψ≥ι―υΖΫΖ®≥ι≥ω100»ΥΉςΫχ“Μ≤ΫΖ÷ΈωΘ§‘ρ‘¬ ’»κ‘Ύ![]() ΒΡ’βΕΈ”Π≥ι»ΓΕύ…Ό»ΥΘΩ
ΒΡ’βΕΈ”Π≥ι»ΓΕύ…Ό»ΥΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΆ÷‘≤![]() ΒΡΉσΓΔ”“ΕΞΒψΖ÷±πΈΣ
ΒΡΉσΓΔ”“ΕΞΒψΖ÷±πΈΣ![]() Θ§
Θ§![]() Θ§«“ΉσΓΔ”“ΫΙΒψ”κΕΧ÷αΒΡ“ΜΗωΕΥΒψ «Β»±Ώ»ΐΫ«–ΈΒΡ»ΐΗωΕΞΒψΘ§Βψ
Θ§«“ΉσΓΔ”“ΫΙΒψ”κΕΧ÷αΒΡ“ΜΗωΕΥΒψ «Β»±Ώ»ΐΫ«–ΈΒΡ»ΐΗωΕΞΒψΘ§Βψ![]() ‘ΎΆ÷‘≤…œΘ§ΙΐΒψ
‘ΎΆ÷‘≤…œΘ§ΙΐΒψ![]() ΒΡ÷±œΏΫΜΆ÷‘≤
ΒΡ÷±œΏΫΜΆ÷‘≤![]() ”Ύ
”Ύ![]() ÷α…œΖΫΒΡΒψ
÷α…œΖΫΒΡΒψ![]() Θ§ΫΜ÷±œΏ
Θ§ΫΜ÷±œΏ![]() ”ΎΒψ
”ΎΒψ![]() .÷±œΏ
.÷±œΏ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() ΒΡΝμ“ΜΫΜΒψΈΣ
ΒΡΝμ“ΜΫΜΒψΈΣ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ”κ÷±œΏ
”κ÷±œΏ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() .
.
Θ®1Θ©«σΆ÷‘≤![]() ΒΡ±ξΉΦΖΫ≥ΧΘΜ
ΒΡ±ξΉΦΖΫ≥ΧΘΜ
Θ®2Θ©»τ![]() Θ§ ‘«σ÷±œΏ
Θ§ ‘«σ÷±œΏ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®3Θ©»γΙϊ![]() Θ§ ‘«σ
Θ§ ‘«σ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫΪ“ΜΩ≈ςΜΉ”œ»Κσ≈Ή÷ά2¥ΈΘ§Ιέ≤λœρ…œΒΡΒψ ΐΘ§«σΘΚ
Θ®1Θ©ΝΫ ΐ÷–÷Ν…Ό”–“ΜΗωΤφ ΐΒΡΗ≈¬ ΘΜ
Θ®2Θ©“‘ΒΎ“Μ¥Έœρ…œΒΡΒψ ΐΈΣΚαΉχ±ξxΘ§ΒΎΕΰ¥Έœρ…œΒΡΒψ ΐΈΣΉίΉχ±ξyΒΡΒψΘ®xΘ§yΘ©‘Ύ‘≤x2+y2ΘΫ15ΒΡΆβ≤ΩΜρ‘≤…œΒΡΗ≈¬ .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com