【答案】
分析:(1)由正弦定理化简已知的等式,得到a,b及c的关系式,根据周长的值,求出c的值即可;
(2)由三角形的面积公式表示出三角形ABC的面积,使其等于已知的面积,得到ab的值,又根据第一问求出的c的值,得到a+b的值,配方后求出a
2+b
2的值,然后利用余弦定理表示出cosC,把得到的a
2+b
2,ab及c的值代入求出cosC的值,由C为三角形的内角,利用特殊角的三角函数值即可得到C的度数.
解答:解:(1)∵△ABC的周长为
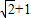
,
∴
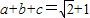
,
∵
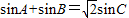
,
∴由正弦定理得
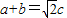
,(2分)
∴c=1;(3分)
(2)∵△ABC的面积
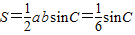
,
∴
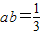
,(4分)
∵
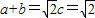
,
∴
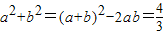
,
∴由余弦定理得
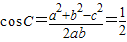
(7分)
∵C∈(0,π),
∴
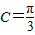
(8分)
点评:此题考查了正弦定理,余弦定理,三角形的面积公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

 ,且
,且
 ,求:角C大小.
,求:角C大小.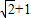 ,
,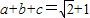 ,
,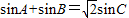 ,
,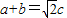 ,(2分)
,(2分)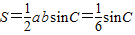 ,
,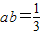 ,(4分)
,(4分)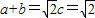 ,
,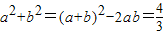 ,
,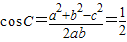 (7分)
(7分)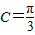 (8分)
(8分)
