Question

已知n为自然数，实数a>1，解关于x的不等式

log_ax－logx＋12logx＋…＋n (n－2)logx>log(x²－a)

Answer 1

解答见解析．

解析:

解：利用对数换底公式，原不等式左端化为

log_ax－4·＋12·＋…＋n(－2)^n－1 ·

  =

故原不等式可化为log_ax>log_a(x²－a)．      ①

当n为奇数时，>0，不等式①等价于log_ax>log_a(x²－a)．     ②

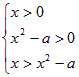
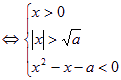
因为a>1，②式等价于 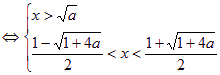——6分

因为<0， >=，

所以，不等式②的解集为{x|<x<}．                    ——8分

当n为偶数时，<0，不等式①等价于log_ax>log_a(x²－a)．           ③

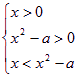
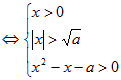
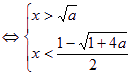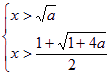因为a>1，③式等价于  或                                                    ——10分

因为                   ——12分

所以，不等式③的解集为{x|x>}．

综合得：当n为奇数时，原不等式的解集是{x|}；

当n为偶数时，原不等式的解集是{x|}