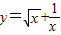Question

下列函数中，奇函数是（ ）
A．y=x²+
B．y=x³，x≠0
C．
D．y=2x，x∈（-2，+∞）

Answer 1

【答案】分析：先求出D，C的定义域，由于定义域不关于原点对称，得到都不是奇函数；对于A，B验证f（-x）与f（x）的关系，判断出B是奇函数．
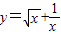
解答：解：对于C，函数的定义域为x＞0，定义域不关于原点对称，故不是奇函数
对于D，定义域为∈（-2，+∞），不关于原点对称，故不是奇函数
对于A，将x换为-x得到y=x²-x，故A不对
对于B，定义域关于原点对称，并且f（-x）=-f（x），故B是奇函数
故选B
点评：判断一个函数是否具有奇偶性，先求出定义域，判断定义域是否关于原点对称，若不关于原点对称函数不具有奇偶性；若关于原点对称，再验证f（-x）与f（x）的关系．