求经过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点,且面积最小的圆的方程.
【答案】
分析:设出所求圆的方程为x
2+y
2+2x-4y+1+λ(2x+y+4=0)=0,找出此时圆心坐标,当圆心在直线2x+y+4=0上时,圆的半径最小,可得此时面积最小,把表示出的圆心坐标代入2x+y+4=0中,得到关于λ的方程,求出方程的解得到λ的值,进而确定出所求圆的方程.
解答:解:可设圆的方程为x
2+y
2+2x-4y+1+λ(2x+y+4=0)=0,
即x
2+y
2+2(1+λ)x+(λ-4)y+4λ+1=0,
此时圆心坐标为(-1-λ,
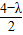
),
显然当圆心在直线2x+y+4=0上时,圆的半径最小,从而面积最小,
∴2(-1-λ)+
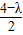
+4=0,
解得:λ=

,
则所求圆的方程为:x
2+y
2+
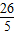
x-
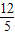
y+
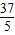
=0.
点评:此题考查了直线与圆相交的性质,根据题意设出所求圆的方程,找出圆心坐标,得出圆心在直线2x+y+4=0上时面积最小是解本题的关键.

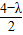 ),
),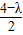 +4=0,
+4=0, ,
,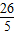 x-
x-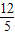 y+
y+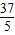 =0.
=0.
