在直角坐标系
中，曲线C的参数方程为
(其中
为参数)，以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系中，直线
的极坐标方程为
.
（Ⅰ）求C的普通方程和直线
的倾斜角；
（Ⅱ）设点
(0，2)，
和
交于
两点，求
.
轻巧夺冠周测月考直通中考系列答案科目：高中数学 来源：2016届山西省等四校高三下第四次联考文科数学试卷（解析版） 题型：选择题
已知双曲线
的左右焦点分别为
，
，若
上存在点
使
为等腰三角形，且其顶角为
，则
的值是（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学 来源：2016届山西省等四校高三下第四次联考理科数学试卷（解析版） 题型：解答题
根据国家《环境空气质量标准》规定:居民区中的PM2.5（PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称可入肺颗粒物）年平均浓度不得超过35微克/立方米，PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据，数据统计如下：
（1）写出该样本的众数和中位数（不必写出计算过程）；
（2）求该样本的平均数，并根据样本估计总体的思想，从PM2.5的年平均浓度考虑，判断该居民区的环境是否需要改进？说明理由；
（3）将频率视为概率，对于去年的某2天，记这2天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为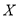
，求
的分布列及数学期望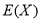
和方差
.
查看答案和解析>>
科目：高中数学 来源：2016届山西省等四校高三下第四次联考理科数学试卷（解析版） 题型：选择题
已知抛物线
的焦点F到双曲线C：
渐近线的距离为
，点P是抛物线上的一动点，P到双曲线C的上焦点
的距离与到直线
的距离之和的最小值为3，则该双曲线的方程为 ( )
A. 
B.
C. 
D. 
查看答案和解析>>
科目：高中数学 来源：2015-2016学年四川省高二下期中理科数学试卷（解析版） 题型：解答题
已知
为抛物线
上一点，点
到直线
的距离为
.
（1）求
的最小值，并求此时点
的坐标；
（2）若点
到抛物线的准线的距离为
，求
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，集合
，则
（ ） 
B.
C. 
D. 
的一条渐近线为
，则双曲线方程为（ ）
B．
C．
D．
，则
=（ ）
B．
C．
D．
为锐角，
，则
的值为__________．