
| 晕机 | 不晕机 | 合计 | |
| 男乘客 | 28 | 28 | 56 |
| 女乘客 | 28 | 56 | 84 |
| 合计 | 56 | 84 | 140 |
| 140(28×56-28×28)2 |
| 56×84×56×84 |
| 35 |
| 9 |


科目:高中数学 来源: 题型:
| n(ad-bc)2 | (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源:2014届吉林省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,
(1)根据以上数据建立一个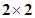 的列联表;(2)能否在犯错误的概率不超过0.05的前提下认为晕机与性别有关?
的列联表;(2)能否在犯错误的概率不超过0.05的前提下认为晕机与性别有关?
查看答案和解析>>
科目:高中数学 来源:2013届湖南省高二上学期期末考试文科数学试卷 题型:填空题
某课外小组在调查男女乘客是否晕机的情况中,获得男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,根据列联表的数据,可以有__________的把握认为晕机与性别有关.
数据列联表:
独立性检验临界值表:
|
P(k2≥k0) |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
|
k0 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
|
]
|
|
晕机 |
不晕机 |
合计 |
|
男乘客 |
28 |
28 |
56 |
|
女乘客 |
28 |
56 |
84 |
|
合计 |
56 |
84 |
140 |
独立性检验随机变量K2值的计算公式: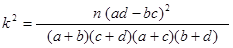
查看答案和解析>>
科目:高中数学 来源:2012届广东省中山市高二下期中考试理科数学试题 题型:解答题
在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是 28人,而女乘客晕机为28人,不会晕机的为56人,
(1)根据以上数据建立一个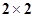 的列联表;
的列联表;
(2)试判断是否晕机与性别有关?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com