
已知函数f(x)=(a2+8)ex,函数g(x)=(x2+ax-2a-3)e3-x.
(1)若a=0,求g(x)的单调递增区间;
(2)若a>0,且存在ξ1,ξ2∈[0,4]使得| f(ξ1)-g(ξ2)|min<3,求实数a的取值范围.
(1)![]() (x)=(2x+a)e3-x-(x2+ax-2a-3)e3-x=e3-x[-x2+(2-a)x+3a+3].
(x)=(2x+a)e3-x-(x2+ax-2a-3)e3-x=e3-x[-x2+(2-a)x+3a+3].
令-x2+(2-a)x+3(a+1)=0,因为a=0,所以当-1<x<3时,![]() (x)>0,
(x)>0,
所以g(x)的单调递增区间为(-1,3). 5分
(2)因为对任意的a值,![]() (x)>0恒成立,所以当a>0时函数f(x)=(a2+8)ex在[0,4]上单调递增,
(x)>0恒成立,所以当a>0时函数f(x)=(a2+8)ex在[0,4]上单调递增,
所以f(x)min=f(0)=a2+8. 7分
令![]() (x)=0,得x1=3,x2=-(a+1).因为a>0,所以x2=-(a+1)<0.
(x)=0,得x1=3,x2=-(a+1).因为a>0,所以x2=-(a+1)<0.

所以g(x)max=g(3)=6+a. 10分
由a2+8>6+a,即f(x)min>g(x)max,所以| f(ξ1)-g(ξ2)|min<3,即a2-a+2<3,
所以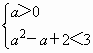 ,解得a∈(0,
,解得a∈(0,![]() ). 13分
). 13分


 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源:2011届南京市金陵中学高三第四次模拟考试数学试题 题型:解答题
(本小题满分16分)已知函数f(x)=ax2-(2a+1)x+2lnx(a为正数).
(1) 若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2) 求f(x)的单调区间;
(3) 设g(x)=x2-2x,若对任意的x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高三上学期开学考试数学卷 题型:选择题
已知函数f(x)=4x2-mx+5在区间[-2,+∞)上是增函数,则f(1)的范围是( )
A.f(1)≥25 B.f(1)=25 C.f(1)≤25 D.f(1)>25
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省天门市高三天5月模拟文科数学试题 题型:填空题
已知函数f(x)=ax2+bx+c(a≠0),且f(x)=x无实根,下列命题中:
(1)方程f [f (x)]=x一定无实根;
(2)若a>0,则不等式f [f (x)]>x对一切实数x都成立;
(3)若a<0,则必存在实数x0,使f [f (x0)]>x0;
(4)若a+b+c=0,则不等式f [f (x)]<x对一切x都成立;
正确的序号有 .
查看答案和解析>>
科目:高中数学 来源:2012届江西省南昌市高三第一次模拟测试卷理科数学试卷 题型:选择题
已知函数f(x)=|lg(x-1)|-( )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有
A.x1x2<1 B.x1x2<x1+x2
C.x1x2=x1+x2 D.x1x2>x1+x2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com