
已知函数f(x)=ex―1―x.
(1)求y=f(x)在点(1,f(1))处的切线方程;
(2)若存在x∈[-1,ln![]() ],使a-ex+1+x<0成立,求a的取值范围;
],使a-ex+1+x<0成立,求a的取值范围;
(3)当x≥0时,f(x)≥tx2恒成立,求t的取值范围.
科目:高中数学 来源:山东省潍坊市2012届高三一轮模拟考试数学文科试题 题型:013
已知函数f(x)=e|lnx|-|x-![]() |,则函数y=f(x+1)的大数图象为
|,则函数y=f(x+1)的大数图象为
A.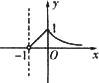
B.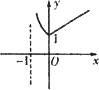
C.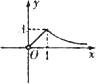
D.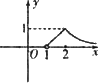
查看答案和解析>>
科目:高中数学 来源:山东省东营市2012届高三一模(3月)数学理科试题 题型:013
已知函数f(x)=e|lnx|-|x-![]() |,则函数y=f(x+1)的大致图象为
|,则函数y=f(x+1)的大致图象为
A.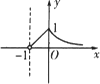
B.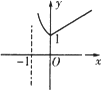
C.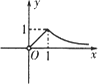
D.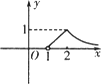
查看答案和解析>>
科目:高中数学 来源:2012年普通高等学校招生全国统一考试上海卷理科数学 题型:022
已知函数f(x)=e|x-a|(a为常数).若f(x)在区间[1,+∞)上是增函数,则a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:北京市海淀区2012届高三5月查漏补缺数学试题 题型:044
已知函数f(x)=e-xsin(其中e=2.718…).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求f(x)在[-π,+∞)上的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com