
如图,由不大于n(n∈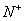 )的正有理数排成的数表,质点按
)的正有理数排成的数表,质点按
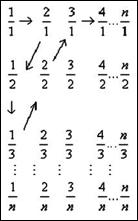
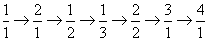
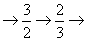 ……顺序跳动,
……顺序跳动,
所经过的有理数依次排列构成数列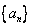 。
。
(Ⅰ)质点从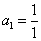 出发,通过抛掷骰子来决定质点的跳动步数,
出发,通过抛掷骰子来决定质点的跳动步数,
骰子的点数为奇数时,质点往前跳一步(从 到达
到达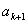 );
);
骰子的点数为偶数时,质点往前跳二步(从 到达
到达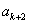 ).
).
①抛掷骰子二次,质点到达的有理数记为ξ,求Eξ;
②求质点恰好到达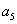 的概率。
的概率。
(Ⅱ)试给出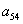 的值(不必写出求解过程)。
的值(不必写出求解过程)。
本题主要考查数列、概率、统计等基础知识,考查数据处理能力、运算求解能力,考查分类与整合思想、化归与转化思想
解:(Ⅰ)①ξ的可能取值为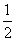 ,
,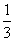 ,
,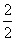
P(ξ=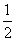 )=
)=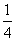 ;P(ξ=
;P(ξ= 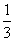 )=
)=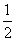 ;P(ξ=
;P(ξ= 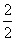 )=
)=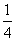 ;
-------------2分
;
-------------2分
ξ的分布列为
|
ξ |
|
|
|
|
P |
|
|
|
Eξ=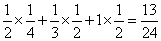 -----------------------------------5分
-----------------------------------5分
②设质点移到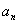 的概率为
的概率为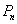 ,质点移到
,质点移到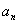 有两种可能:①质点先到
有两种可能:①质点先到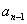 ,骰子掷出的点数为奇数,质点到达
,骰子掷出的点数为奇数,质点到达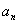 ,其概率为
,其概率为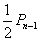 ;②质点先到
;②质点先到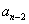 ,骰子掷出的点数为偶数,其概率为
,骰子掷出的点数为偶数,其概率为 。
。
即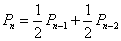 (n≥4)
(n≥4)
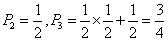
∴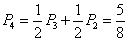
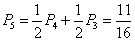 --------------------------------------10分
--------------------------------------10分
法2:质点恰好到达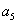 有三种情形
有三种情形
①抛掷骰子四次,出现点数全为奇数,概率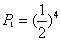 ;
;
②抛掷骰子三次,出现点数二次为奇数,一次为偶数概率为 ;
;
③抛掷骰子二次,出现点数全为偶数,概度为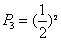 ,故质点恰好到达
,故质点恰好到达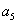 的概
的概
率 ------------------------------------10分
------------------------------------10分
(Ⅱ)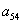 =
=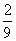 ……………………………………13分
……………………………………13分


科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2010年福建省龙岩市高三第二次质检数学试题(理) 题型:解答题
(本小题满分13分)如图,由不大于n(n∈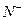 )的正有理数排成的数表,质点按
)的正有理数排成的数表,质点按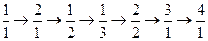
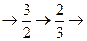 ……顺序跳动,
……顺序跳动,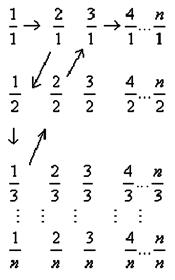
所经过的有理数依次排列构成数列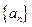 。K^S*5U.C#O
。K^S*5U.C#O
(Ⅰ)质点从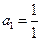 出发,通过抛掷骰子来决定质点的跳动步数,骰子的点数为奇数时,质点往前跳一步(从
出发,通过抛掷骰子来决定质点的跳动步数,骰子的点数为奇数时,质点往前跳一步(从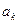 到达
到达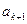 );骰子的点数为偶数时,质点往前跳二步(从
);骰子的点数为偶数时,质点往前跳二步(从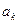 到达
到达 ).
).
①抛掷骰子二次,质点到达的有理数记为ξ,求Eξ;②求质点恰好到达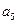 的概率。K^S*5U.C#O
的概率。K^S*5U.C#O
(Ⅱ)试给出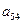 的值(不必写出求解过程)。
的值(不必写出求解过程)。
查看答案和解析>>
科目:高中数学 来源:2011年江苏省淮安市洪泽中学高考数学模拟试卷(3)(解析版) 题型:解答题

 (b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
(b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:2010年江苏省连云港市东海高级中学高考数学考前猜题试卷(4)(解析版) 题型:解答题

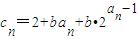 (b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
(b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com