
(1)求证:A1B∥ 面B1DE;
(2)若底面边长为1,侧棱长为![]() .求AB1与平面B1DE所成角.
.求AB1与平面B1DE所成角.
(1)证明:取AD中点F,连BF、A1F
则BF∥DE,∴BF∥面B1DE
且EF![]() AB
AB![]() A1B1,∴EFA1B1是平行四边形
A1B1,∴EFA1B1是平行四边形
∴A1F∥面B1DE
∴面A1FB∥面B1DE
∴A1B∥面B1DE
(2)以D1为原点,D1A1为x轴,D1C1为y轴,D1D为z轴建立直角坐标系
则B1(1,1,0) E(![]() ,1,
,1,![]() ) D(0,0,
) D(0,0,![]() ) A(1,0,
) A(1,0,![]() )
)
∴![]() =(-
=(-![]() ,0,
,0,![]() ),
),![]() =(-1,-1,
=(-1,-1, ![]() ).
).
![]() =(0,-1,
=(0,-1,![]() )
)
设平面B1DE的法向量n=(1,y,z)
∴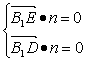
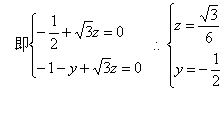
∴n=(1,-![]() ,
,![]() )
)
设AB1与平面B1DE所成角为θ
则sinθ=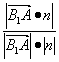
=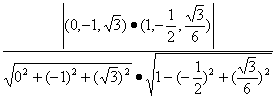
=![]()
∴θ=arcsin![]() .
.
(2)另解:设A到面B1DE的距离为h.
则![]()
∵S△ADE=![]() ,
,
B1B⊥面ADE,且B1B=![]() .
.
又在△B1DE中.
DE=![]()
B1E=![]() .
.
B1D=![]()
∴cos∠B1DE=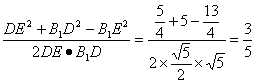
∴sin∠B1DE=![]()
∴![]() =
=![]() sin∠B1DE
sin∠B1DE
=![]()
∴![]() h·1=
h·1=![]() ·
·![]()
又AB1=![]() ,设AB1与平面B1DE所成的角为θ
,设AB1与平面B1DE所成的角为θ
则sinθ=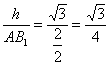
∴θ=arcsin![]()


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
 已知(如图)在正三棱柱(底面正三角形,侧棱垂直于底面)ABC-A1B1C1中,若AB=AA1=4,点D是AA1的中点,点P是BC1中点
已知(如图)在正三棱柱(底面正三角形,侧棱垂直于底面)ABC-A1B1C1中,若AB=AA1=4,点D是AA1的中点,点P是BC1中点查看答案和解析>>
科目:高中数学 来源: 题型:
 (文科)已知正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4,点M在线段CC1上.
(文科)已知正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4,点M在线段CC1上.| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
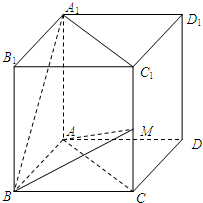 (文科)已知正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4,点M在线段CC1上.
(文科)已知正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4,点M在线段CC1上. ,求多面体ABM-A1B1C1的体积.
,求多面体ABM-A1B1C1的体积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com