
已知函数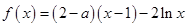 ,
,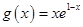 (
(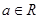 ,
,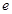 为自然对数的底数).
为自然对数的底数).
(1)当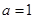 时,求
时,求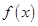 的单调区间;
的单调区间;
(2)对任意的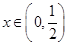 ,
,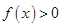 恒成立,求
恒成立,求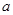 的最小值;
的最小值;
(3)若对任意给定的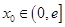 ,在
,在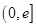 上总存在两个不同的
上总存在两个不同的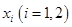 ,使得
,使得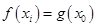 成立,求
成立,求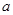 的取值范围.
的取值范围.
(1)函数 的单调减区间为
的单调减区间为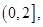 单调增区间为
单调增区间为 ;(2)实数
;(2)实数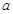 的最小值为
的最小值为 ;
;
(3)实数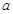 的取值范围是
的取值范围是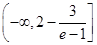 .
.
【解析】
试题分析:(1)把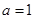 代入函数
代入函数 的解析式,直接利用导数求函数
的解析式,直接利用导数求函数 在定义域上的单调区间;(2)利用参数分离法将问题中的不等式等价转化为
在定义域上的单调区间;(2)利用参数分离法将问题中的不等式等价转化为 在
在 上恒成立,即
上恒成立,即 ,进而求出参数
,进而求出参数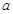 的取值范围,从而求出
的取值范围,从而求出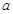 的最小值;(3)先利用导数求出函数
的最小值;(3)先利用导数求出函数 在
在 上的值域,利用导数研究函数
上的值域,利用导数研究函数 的单调性,并求出方程
的单调性,并求出方程 的唯一根
的唯一根 ,将条件“对于任意给定的
,将条件“对于任意给定的
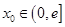 ,在
,在 总存在两个不同的
总存在两个不同的 ,使得
,使得 ”转化为“函数
”转化为“函数 在区间
在区间 上存在唯一极值点
上存在唯一极值点 ,即
,即 ,且函数
,且函数 在区间
在区间 和区间
和区间 上的值域均包含函数
上的值域均包含函数 在区间
在区间 上的值域”,从而列出相应的不等式进行求解参数
上的值域”,从而列出相应的不等式进行求解参数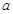 的取值范围.
的取值范围.
试题解析:(1)当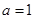 时,
时, ,
, ,
,
由 ,
, ,由
,由 ,
,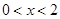 ,
,
故 的单调减区间为
的单调减区间为 ,单调增区间为
,单调增区间为 ;
;
(2)即对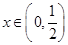 ,
, 恒成立,
恒成立,
令 ,
,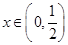 ,则
,则 ,
,
再令 ,
,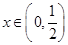 ,
, ,
,
 在
在 上为减函数,于是
上为减函数,于是 ,
,
从而,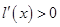 ,于是
,于是 在
在 上为增函数,
上为增函数, ,
,
故要 恒成立,只要
恒成立,只要 ,即
,即 的最小值为
的最小值为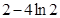 ;
;
(3)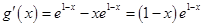 ,当
,当 时,
时, ,函数
,函数 单调递增,
单调递增,
当 时,
时,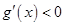 ,函数
,函数 单调递减,
单调递减,
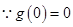 ,
, ,
, ,
,
所以,函数 在
在 上的值域为
上的值域为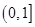 .
.
当 时,不合题意;
时,不合题意;
当 时,
时,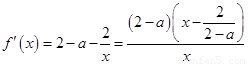 ,
, ,
,
故 ,
, , ①
, ①
此时,当 变化时,
变化时, 、
、 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
|
|
|
|
单调减 |
最小值 |
单调增 |
 ,
,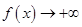 ,
, ,
, ,
,
所以,对任意给定的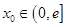 ,在区间
,在区间 上总存在两个不同的
上总存在两个不同的 ,
,
使得 成立,当且仅当
成立,当且仅当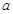 满足下列条件
满足下列条件
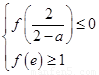 ,即
,即
令 ,
,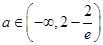 ,
,
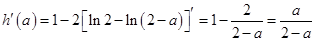 ,令
,令 ,得
,得 ,
,
当 时,
时, ,函数
,函数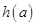 单调递增,
单调递增,
当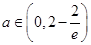 时,
时, ,函数
,函数 单调递减,
单调递减,
所以,对任意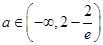 ,有
,有 ,
,
即②对任意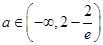 恒成立,
恒成立,
由③式解得: , ④
, ④
综合①④可知,当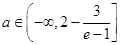 时,对任意给定的
时,对任意给定的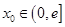 ,
,
在 总存在两个不同的
总存在两个不同的 ,使得
,使得 成立.
成立.
考点:1.函数的单调区间;2.不等式恒成立;3.参数分离法;4.函数值域的包含关系


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年广东省高三第二次段考文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知函数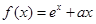 ,
,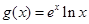 .(其中
.(其中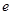 为自然对数的底数),
为自然对数的底数),
(Ⅰ)设曲线 在
在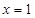 处的切线与直线
处的切线与直线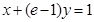 垂直,求
垂直,求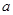 的值;
的值;
(Ⅱ)若对于任意实数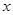 ≥0,
≥0,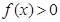 恒成立,试确定实数
恒成立,试确定实数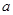 的取值范围;
的取值范围;
(Ⅲ)当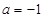 时,是否存在实数
时,是否存在实数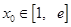 ,使曲线C:
,使曲线C: 在点
在点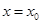
处的切线与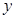 轴垂直?若存在,求出
轴垂直?若存在,求出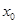 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省等三校高三2月月考数学文卷 题型:解答题
(本小题满分14分)
已知函数 ,
, .(其中
.(其中 为自然对数的底数),
为自然对数的底数),
(Ⅰ)设曲线 在
在 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;
(Ⅱ)若对于任意实数 ≥0,
≥0, 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(Ⅲ)当 时,是否存在实数
时,是否存在实数 ,使曲线C:
,使曲线C: 在点
在点
处的切线与 轴垂直?若存在,求出
轴垂直?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012届福建省福州市高二期末理科考试数学试卷 题型:解答题
已知函数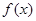 =
=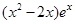 (e为自然对数的底数)
(e为自然对数的底数)
(Ⅰ)求函数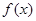 单调递增区间;(5分)
单调递增区间;(5分)
(Ⅱ)若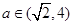 ,求函数
,求函数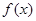 在区间[0,
在区间[0,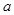 ]上的最大值和最小值.(5分)
]上的最大值和最小值.(5分)
(III) 若函数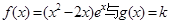 的图象有三个不同的交点,求实数k的取值范围.
的图象有三个不同的交点,求实数k的取值范围.
(参考数据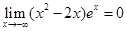 )(2分)
)(2分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com