2

-2<m<8 7
分析:A 把直线l的参数方程化为直角坐标方程为 3x-4y-8=0,曲线C的参数方程化为直角坐标方程为(x-5)
2+(y-3)
2=4,表示以(5,3)为圆心,以2为半径的圆,求出圆心到直线的距离,再利用弦长公式求出弦长.
B|x-3|+|x-m|表示数轴上的x对应点到3和m对应点的距离之和,其最小值为|m-3|,由|m-3|<5,解得实数m的取值范围.
C 设R,r分别为Rt△ABC的外接圆半径和内切圆半径,则由直角三角形的内切圆与外接圆的面积分别π与9π可得 r=1,R=3.设两直角边分别为a,b,则由圆的切线性质可得斜边为
a-r+b-r=
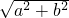
=2R=6,解得 a+b=8,根据三角形的面积等于
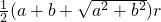
求得结果.
解答:A 直线l:
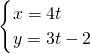
(t为参数)即
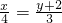
,即 3x-4y-8=0.
曲线C:

(θ为参数)化为直角坐标方程为(x-5)
2+(y-3)
2=4,表示以(5,3)为圆心,以2为半径的圆.
圆心到直线的距离等于
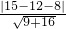
=1,由弦长公式求得弦长为2
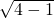
=2

,
故答案为 2

.
B 由于存在实数x满足|x-3|+|x-m|<5,而|x-3|+|x-m|表示数轴上的x对应点到3和m对应点的距离之和,其最小值为|m-3|,
故|m-3|<5,解得-2<m<8,
故答案为-2<m<8.
C 设R,r分别为Rt△ABC的外接圆半径和内切圆半径,则由直角三角形的内切圆与外接圆的面积分别π与9π可得 πr
2=π,πR
2=9π,
解得 r=1,R=3.
设两直角边分别为a,b,则由圆的切线性质可得斜边为 a-r+b-r=
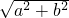
=2R=6,∴a+b=8.
故三角形的面积等于
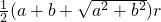
=

=7,
故答案为 7.
点评:本题考查了把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用.解绝对值不等式,绝对值的意义.三角形的内切圆和内心,以及外心的定义和求法,属于中档题.

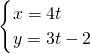 (t为参数)被曲线C:
(t为参数)被曲线C: (θ为参数)所截得的弦长为________.
(θ为参数)所截得的弦长为________. -2<m<8 7
-2<m<8 7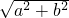 =2R=6,解得 a+b=8,根据三角形的面积等于
=2R=6,解得 a+b=8,根据三角形的面积等于 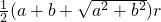 求得结果.
求得结果.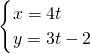 (t为参数)即
(t为参数)即 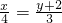 ,即 3x-4y-8=0.
,即 3x-4y-8=0. (θ为参数)化为直角坐标方程为(x-5)2+(y-3)2=4,表示以(5,3)为圆心,以2为半径的圆.
(θ为参数)化为直角坐标方程为(x-5)2+(y-3)2=4,表示以(5,3)为圆心,以2为半径的圆.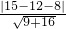 =1,由弦长公式求得弦长为2
=1,由弦长公式求得弦长为2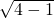 =2
=2 ,
, .
.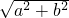 =2R=6,∴a+b=8.
=2R=6,∴a+b=8.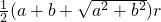 =
= =7,
=7,

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案 (t为参数)被曲线C:
(t为参数)被曲线C: (θ为参数)所截得的弦长为 .
(θ为参数)所截得的弦长为 .