
 现在小型轿车慢慢进入百姓家庭,但是另一个问题相继暴露出来--堵车.李先生居住在城市的A处,准备开车到B处上班,若该地各路段发生堵车事件是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图所示(例如A→C→D并作两个路段:路段AC发生堵车事件的概率是
现在小型轿车慢慢进入百姓家庭,但是另一个问题相继暴露出来--堵车.李先生居住在城市的A处,准备开车到B处上班,若该地各路段发生堵车事件是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图所示(例如A→C→D并作两个路段:路段AC发生堵车事件的概率是| 1 |
| 10 |
| 1 |
| 15 |
. |
| G |
. |
| H |
. |
| J |
. |
| G |
. |
| H |
. |
| J |
| 9 |
| 10 |
| 14 |
| 15 |
| 5 |
| 6 |
| 3 |
| 10 |
| 3 |
| 10 |
| 89 |
| 320 |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 504 |
| 720 |
| 7 |
| 10 |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 191 |
| 720 |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 24 |
| 720 |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 1 |
| 720 |
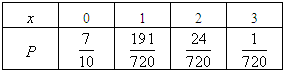
| 7 |
| 10 |
| 191 |
| 720 |
| 24 |
| 720 |
| 1 |
| 720 |
| 242 |
| 720 |
| 121 |
| 360 |


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com